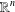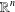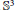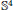14 results
Catenaries and minimal surfaces of revolution in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Total mean curvature surfaces in the product space
 ${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
${\mathbb{S}^{n}\times\mathbb{R}}$ and applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 346-365
-
- Article
- Export citation
8 - Constrained Willmore Surfaces and the Isothermic Surface Condition
-
- Book:
- Constrained Willmore Surfaces
- Published online:
- 13 May 2021
- Print publication:
- 10 June 2021, pp 145-182
-
- Chapter
- Export citation

Constrained Willmore Surfaces
- Symmetries of a Möbius Invariant Integrable System
-
- Published online:
- 13 May 2021
- Print publication:
- 10 June 2021
NEW COMPLEX ANALYTIC METHODS IN THE THEORY OF MINIMAL SURFACES: A SURVEY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 23 August 2018, pp. 287-341
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A Note on a Unicity Theorem for the Gauss Maps of Complete Minimal Surfaces in Euclidean Four-space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 292-300
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
Simulation of a Soap Film Möbius Strip Transformation
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 615-628
- Print publication:
- August 2017
-
- Article
- Export citation
A Two-Stage Image Segmentation Model for Multi-Channel Images
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 904-926
- Print publication:
- April 2016
-
- Article
- Export citation
Function-theoretic Properties for the Gauss Maps of Various Classes of Surfaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 6 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1411-1434
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Spectral Properties of a Family of Minimal Tori of Revolution in the Five-dimensional Sphere
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 285-296
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation
ON MINIMAL SURFACES SATISFYING THE OMORI–YAU PRINCIPLE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 33-39
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
THE DIRICHLET PROBLEM FOR THE MINIMAL SURFACES EQUATION AND THE PLATEAU PROBLEM AT INFINITY
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 3 / Issue 3 / July 2004
- Published online by Cambridge University Press:
- 01 July 2004, pp. 397-420
- Print publication:
- July 2004
-
- Article
- Export citation
PROPERLY EMBEDDED MINIMAL ANNULI BOUNDED BY A CONVEX CURVE
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 1 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 24 January 2003, pp. 293-305
- Print publication:
- April 2002
-
- Article
- Export citation
Self θ-congruent minimal surfaces in ℝ3
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-244
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation