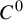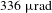7 results
Density of mode-locking property for quasi-periodically forced Arnold circle maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 04 April 2024, pp. 3645-3680
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
7 - Quantum Cascade Laser Frequency Combs
- from Part II - Active Research Topics
-
- Book:
- Mid-Infrared and Terahertz Quantum Cascade Lasers
- Published online:
- 25 August 2023
- Print publication:
- 14 September 2023, pp 203-248
-
- Chapter
- Export citation
2.1 \unicode{x3bc}m, high-energy dissipative soliton resonance from a holmium-doped fiber laser system
-
- Journal:
- High Power Laser Science and Engineering / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 January 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Applications of Fibre Amplifiers and Lasers in Spectroscopy
-
- Book:
- Laser and Fiber Optic Gas Absorption Spectroscopy
- Published online:
- 07 April 2021
- Print publication:
- 08 April 2021, pp 198-231
-
- Chapter
- Export citation
6 - Principles of Fibre Amplifiers and Lasers for Near-IR Spectroscopy
-
- Book:
- Laser and Fiber Optic Gas Absorption Spectroscopy
- Published online:
- 07 April 2021
- Print publication:
- 08 April 2021, pp 159-197
-
- Chapter
- Export citation
Tunable optical frequency comb from a compact and robust Er:fiber laser
-
- Journal:
- High Power Laser Science and Engineering / Volume 8 / 2020
- Published online by Cambridge University Press:
- 07 May 2020, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Two-micron all-fiberized passively mode-locked fiber lasers with high-energy nanosecond pulse
-
- Journal:
- High Power Laser Science and Engineering / Volume 8 / 2020
- Published online by Cambridge University Press:
- 29 April 2020, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation