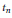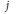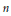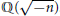Refine search
Actions for selected content:
8 results
2-Elongated plane partitions and powers of 7: the localization method applied to a genus 1 congruence family
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 August 2025, pp. 1-43
-
- Article
- Export citation
There are at most finitely many singular moduli that are S-units
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 732-770
- Print publication:
- April 2024
-
- Article
- Export citation
CONGRUENCES FOR RANKS OF PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 280-290
- Print publication:
- October 2024
-
- Article
- Export citation
NORMAL BASES FOR MODULAR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 384-392
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
On some Fricke families and application to the Lang–Schertz conjecture
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 18 May 2016, pp. 723-740
- Print publication:
- August 2016
-
- Article
- Export citation
Some applications of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 03 June 2015, pp. 91-106
-
- Article
- Export citation
Algebraic integers as special values of modular units
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 01 November 2011, pp. 167-179
-
- Article
-
- You have access
- Export citation
Ramanujan and the Modular j-Invariant
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 4 / 01 December 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 427-440
- Print publication:
- 01 December 1999
-
- Article
-
- You have access
- Export citation

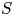
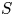
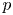
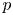
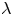
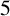
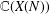
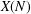
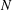
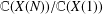
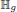 .
.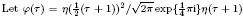 , where
, where 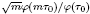 is an algebraic integer dividing
is an algebraic integer dividing 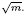 This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when
This is a generalization of a result of Berndt, Chan and Zhang. On the other hand, when 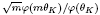 is a unit.
is a unit.