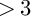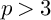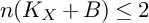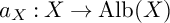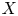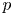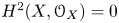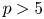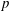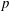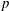15 results
NON-LOG LIFTABLE LOG DEL PEZZO SURFACES OF RANK ONE IN CHARACTERISTIC FIVE
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-24
-
- Article
- Export citation
NOTE ON THE THREE-DIMENSIONAL LOG CANONICAL ABUNDANCE IN CHARACTERISTIC
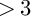 $>3$
$>3$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 694-723
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
On the Bezrukavnikov–Kaledin quantization of symplectic varieties in characteristic p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 January 2024, pp. 411-450
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
Projective varieties with nef tangent bundle in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1974-1999
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - Boundedness of semistable sheaves
-
-
- Book:
- Stacks Project Expository Collection
- Published online:
- 06 October 2022
- Print publication:
- 27 October 2022, pp 126-162
-
- Chapter
- Export citation
On the Kawamata–Viehweg vanishing theorem for log del Pezzo surfaces in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 13 June 2022, pp. 750-763
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON DEL PEZZO FIBRATIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 30 March 2020, pp. 197-239
- Print publication:
- January 2022
-
- Article
- Export citation
Dirichlet's Theorem in Function Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 532-547
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
On log del Pezzo surfaces in large characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 820-850
- Print publication:
- April 2017
-
- Article
- Export citation
The
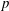 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 10 June 2014, pp. 1125-1168
- Print publication:
- July 2014
-
- Article
- Export citation
Monoidal transforms and invariants of singularities in positive characteristic
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 19 June 2013, pp. 1267-1311
- Print publication:
- August 2013
-
- Article
- Export citation
On the S-fundamental group scheme. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 02 April 2012, pp. 835-854
- Print publication:
- October 2012
-
- Article
- Export citation
Rational functions with given ramification in characteristic p
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 13 March 2006, pp. 433-450
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
A remark on semi-stable fibrations over $P^1$ in positive characteristic
-
- Journal:
- Compositio Mathematica / Volume 112 / Issue 1 / May 1998
- Published online by Cambridge University Press:
- 04 December 2007, pp. 41-44
- Print publication:
- May 1998
-
- Article
-
- You have access
- Export citation
Enumerative Geometry for Plane Cubic Curves in Characteristic 2
-
- Journal:
- Compositio Mathematica / Volume 111 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 04 December 2007, pp. 123-147
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation