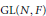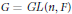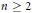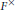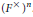2 results
Transfert du pseudo-coefficient de Kottwitz et formules de caractère pour la série discrète de GL(N) sur un corps local
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 2 / 01 April 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-283
- Print publication:
- 01 April 2014
-
- Article
-
- You have access
- Export citation
Intégrales orbitales tordues sur GL(n, F) et corps locaux proches : applications
-
- Journal:
- Canadian Journal of Mathematics / Volume 58 / Issue 6 / 01 December 2006
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1229-1267
- Print publication:
- 01 December 2006
-
- Article
-
- You have access
- Export citation