Simulating plasma physics on quantum computers is difficult because most problems of interest are nonlinear, but quantum computers are not naturally suitable for nonlinear operations. In weakly nonlinear regimes, plasma problems can be modelled as wave–wave interactions. In this paper, we develop a quantization approach to convert nonlinear wave–wave interaction problems to Hamiltonian simulation problems. We demonstrate our approach using two qubits on a superconducting device. Unlike a photonic device, a superconducting device does not naturally have the desired interactions in its native Hamiltonian. Nevertheless, Hamiltonian simulations can still be performed by decomposing required unitary operations into native gates. To improve experimental results, we employ a range of error-mitigation techniques. Apart from readout error mitigation, we use randomized compilation to transform undiagnosed coherent errors into well-behaved stochastic Pauli channels. Moreover, to compensate for stochastic noise, we rescale exponentially decaying probability amplitudes using rates measured from cycle benchmarking. We carefully consider how different choices of product-formula algorithms affect the overall error and show how a trade-off can be made to best utilize limited quantum resources. This study provides an example of how plasma problems may be solved on near-term quantum computing platforms.

The quantum three-wave interaction, the lowest-order nonlinear interaction in plasma physics, describes energy–momentum transfer between three resonant waves in the quantum regime. We describe how it may also act as a finite-degree-of-freedom approximation to the classical three-wave interaction in certain circumstances. By promoting the field variables to operators, we quantize the classical system, show that the quantum system has more free parameters than the classical system and explain how these parameters may be selected to optimize either initial or long-term correspondence. We then numerically compare the long-time quantum–classical correspondence far from the fixed point dynamics. We discuss the Poincaré recurrence of the system and the mitigation of quantum scrambling.

Spontaneous avalanche to plasma begins in the core of an ellipsoidal Rydberg gas of nitric oxide. Ambipolar expansion of NO$^+$ draws energy from avalanche-heated electrons. Then, cycles of long-range resonant electron transfer from Rydberg molecules to ions equalize their relative velocities. This sequence of steps gives rise to a remarkable mechanics of self-assembly, in which the kinetic energy of initially formed hot electrons and ions drives an observed separation of plasma volumes. These dynamics adiabatically sequester energy in a reservoir of mass transport, starting a process that anneals separating volumes to form an apparent glass of strongly coupled ions and electrons. Short-time electron spectroscopy provides experimental evidence for complete ionization. The long lifetime of this system, particularly its stability with respect to recombination and neutral dissociation, suggests that this transformation affords a robust state of arrested relaxation, far from thermal equilibrium. We see this most directly in the excitation spectrum of transitions to states in the initially selected Rydberg series, detected as the long-lived signal that survives a flight time of $500\ \mathrm {\mu }$s to reach an imaging detector. The initial density of electrons produced by prompt Penning ionization, which varies with the selected initial principal quantum number and density of the Rydberg gas, determines a balance between the rising density of ions and the falling density of Rydberg molecules. This Penning-regulated ion-Rydberg molecule balance appears necessary as a critical factor in achieving the long ultracold plasma lifetime to produce spectral features detected after very long delays.

We present a theoretical study of two- and three-dimensional massless Dirac one-component plasmas embedded in a constant uniform magnetic field. We determine the wavefunctions and Landau energy levels of a massless Dirac fermion in a constant magnetic field. On this basis we consider magnetism of Fermi fluids of massless charged particles. We show that such a three-dimensional Dirac plasma consisting of fermions with the same helicity has its own magnetic moment. We also consider the limit of strong magnetic fields and investigate the De Haas–van Alphen effect. We derive the Kubo formula for the electrical conductivity tensor of massless Dirac plasmas and consider the Shubnikov–de Haas effect. In addition, we propose a model of the static conductivity tensor and employ the matrix version of the classical method of moments to derive a Drude-like formula for the dynamic conductivity tensor for massless Dirac plasmas. We find that the electrical conductivity tensor for Dirac fermions with the right helicity is not isotropic in the plane perpendicular to the magnetic field.

We present a numerical method to solve the Vlasov–Maxwell equations for spin-1/2 particles, in a semiclassical approximation where the orbital motion is treated classically while the spin variable is fully quantum. Unlike the spinless case, the phase-space distribution function is a $2\times 2$ matrix, which can also be represented, in the Pauli basis, as one scalar function $f_0$ and one three-component vector function $\boldsymbol f$. The relationship between this ‘vectorial’ representation and the fully scalar representation on an extended phase space first proposed by Brodin et al. (Phys. Rev. Lett., vol. 101, 2008, p. 245002) is analysed in detail. By means of suitable approximations and symmetries, the vectorial spin-Vlasov–Maxwell model can be reduced to two-dimensions in the phase space, which is amenable to numerical solutions using a high-order grid-based Eulerian method. The vectorial model enjoys a Poisson structure that paves the way to accurate Hamiltonian split-time integrators. As an example, we study the stimulated Raman scattering of an electromagnetic wave interacting with an underdense plasma, and compare the results with those obtained earlier with the scalar spin-Vlasov–Maxwell model and a particle-in-cell code.

The propagation of extraordinary and upper-hybrid waves in spin quantum magnetoplasmas with vacuum polarization effect is investigated. Based on the quantum magnetohydrodynamics model including Bohm potential, arbitrary relativistic degeneracy pressure and spin force, and Maxwell's equations modified by the spin current and vacuum polarization current, the dispersion relations of extraordinary and upper-hybrid waves are derived. The analytical and numerical results show that quantum effects (Bohm potential, degeneracy pressure and spin magnetization energy) and the vacuum polarization effect modify the propagation of the extraordinary wave. Under the action of a strong magnetic field, the plasma frequency is obviously increased by the vacuum polarization effect.

We propose a numerical scheme to solve the semiclassical Vlasov–Maxwell equations for electrons with spin. The electron gas is described by a distribution function $f(t,{\boldsymbol x},{{{\boldsymbol p}}}, {\boldsymbol s})$ that evolves in an extended 9-dimensional phase space $({\boldsymbol x},{{{\boldsymbol p}}}, {\boldsymbol s})$, where $\boldsymbol s$ represents the spin vector. Using suitable approximations and symmetries, the extended phase space can be reduced to five dimensions: $(x,{{p_x}}, {\boldsymbol s})$. It can be shown that the spin Vlasov–Maxwell equations enjoy a Hamiltonian structure that motivates the use of the recently developed geometric particle-in-cell (PIC) methods. Here, the geometric PIC approach is generalized to the case of electrons with spin. Total energy conservation is very well satisfied, with a relative error below $0.05\,\%$. As a relevant example, we study the stimulated Raman scattering of an electromagnetic wave interacting with an underdense plasma, where the electrons are partially or fully spin polarized. It is shown that the Raman instability is very effective in destroying the electron polarization.

The propagation characteristics of linear waves in high-energy-density magnetoplasmas are investigated using a relativistic magnetohydrodynamic model based on the framework of relativistic quantum theory. Based on the covariant Wigner function approach, a relativistic quantum magnetohydrodynamic model is established. Starting from the relativistic quantum magnetohydrodynamic equations and the Maxwell equations, the dispersion equation for relativistic quantum magnetoplasmas is derived. The contributions of both quantum effects and relativistic effects are shown in the dispersion relations for perpendicular, parallel propagation with respect to a background magnetic field. Results show that the corrections of both quantum effects and relativistic effects are significant when choosing the plasma parameters of laser-based plasma compression schemes.

We present a Monte Carlo collisional scheme that models single Compton scattering between leptons and photons in particle-in-cell codes. The numerical implementation of Compton scattering can deal with macro-particles of different weights and conserves momentum and energy in each collision. Our scheme is validated through two benchmarks for which exact analytical solutions exist: the inverse Compton spectra produced by an electron scattering with an isotropic photon gas and the photon–electron gas equilibrium described by the Kompaneets equation. It provides new opportunities for numerical investigation of plasma phenomena where a significant population of high-energy photons is present in the system.

We have investigated the influence of a strong magnetic field on various aspects of a quantum Fermi plasma. Due to the strong magnetic field, the distribution function becomes anisotropic. First, we consider non-degenerate quantum, Landau and Kelly distribution function. It was found that the adiabatic equation is similar to the adiabatic equation for a Maxwell distribution function, when we include the magnetic field in the energy expression. Using the Kelly distribution for a degenerate, quantum Fermi gas, parallel and perpendicular components of the pressure were derived. It was found that perpendicular component of pressure never becomes zero and three-dimensional system always stay three-dimensional. Lastly, we investigated electron emission from metals and have shown the influence of the magnetic field. We calculated thermionic emission, the so-called Richardson effect. In addition, we investigate the influence of external electromagnetic radiation on the electron current density (Hallwachs effect) from metals.

The possibilities of surface plasma wave (SPW) on a metal-vacuum interface in semiconductor quantum plasma by considering the effects of Coulomb exchange (CE) interaction and the spin-polarization has been explored. The dispersion for the SPW has been setup using the modified quantum hydrodynamic (QHD) model taking into account the Fermi pressure, the quantum Bohm force, the CE, and the electron spin. The optical gain of SPW has been evaluated. It is found that CE effects and spin-polarization increases the wave frequency and enhances the gain during the stimulated emission.

Magnetic field quantization is an important issue for degenerate environments such as neutron stars, radio pulsars and magnetars etc., due to the fact that these stars have a magnetic field higher than the quantum critical field strength of the order of 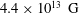$4.4\times 10^{13}~\text{G}$, accordingly, the cyclotron energy may be equal to or even much more than the Fermi energy of degenerate particles. We shall formulate here the exotic physics of strongly magnetized neutron stars, known as pulsars, specifically focusing on the outcomes of the quantized magnetic pressure. In this scenario, while following the modified quantum hydrodynamic model, we shall investigate both linear and nonlinear fast magnetosonic waves in a strongly magnetized, weakly ionized degenerate plasma consisting of neutrons and an electron–ion plasma in the atmosphere of a pulsar. Here, linear analysis depicts that sufficiently long, fast magnetosonic waves may exist in a weakly dispersive pulsar having finite phase speed at cutoff. To investigate one-dimensional nonlinear fast magnetosonic waves, a neutron density expression as a function of both the electron magnetic and neutron degenerate pressures, is derived with the aid of Riemann’s wave solution. Consequently, a modified Korteweg–de Vries equation is derived, having a rarefractive solitary wave solution. It is found that the basic properties such as amplitude, width and phase speed of the fast magnetoacoustic waves are significantly altered by the electron magnetic and the neutron degenerate pressures. The results of this theoretical investigation may be useful for understanding the formation and features of the solitary structures in astrophysical compact objects such as pulsars, magnetars and white dwarfs etc.

Nonlinear propagation of ion acoustic waves has been studied in unmagnetized quantum (degenerate) plasma in the presence of an ion beam using the one-dimensional quantum hydrodynamic model. The Korteweg–de Vries (K–dV) equation has been derived by using the reductive perturbation technique. The solution of ion acoustic solitary waves is obtained from the K–dV equation. The theoretical results have been analyzed numerically for different values of plasma parameters and the results are presented graphically. It is seen that the formation and structure of solitary waves are significantly affected by the ion beam in quantum plasma. The solitary waves will be compressive or rarefactive depending upon the values of velocity, concentration, and temperature of the ion beam. The critical value of ion beam density for the nonexistence of solitary wave has been numerically estimated, and its variation with velocity and temperature of ion beam has been discussed graphically. The results are new and would be very useful for understanding the beam–plasma interactions and the formation of nonlinear wave structures in dense quantum plasma.

Study of even harmonic generation resulting from propagation of whistler pulse in homogeneous high-density quantum plasma immersed in an externally applied magnetic field, using the recently developed quantum hydrodynamic model is presented. The effects of quantum Bohm potential, quantum statistical pressure, and electron spin have been taken into account. The field amplitude of even harmonic of the whistler with respect to fundamental wave and the conversion efficiency for phase-mismatch has been analyzed. The conversion efficiency of harmonic radiation depends on the plasma electron density, magnetic field strength as well as the intensity of whistler pulse. The efficiency increases significantly with an increase in plasma density, magnetic field and whistler wave intensity. Higher conversion efficiency is observed in degenerate plasma for lower values of the static magnetic field as compared with classical plasma.

An introduction to the physical interpretation of the Coulomb logarithm is given with particular emphasis on the quantum-mechanical corrections that are required at high temperatures. Excerpts from the literature are used to emphasize the historical understanding of the topic, which emerged more than a half-century ago. Several misinterpretations are noted. Quantum-mechanical effects are related to diffraction by scales of the order of the Debye screening length; they are not due to quantum uncertainty related to the much smaller distance of closest approach.

We examine the properties of linear electrostatic waves in unmagnetised quantum and classical plasmas consisting of one or two populations of electrons with analytically tractable distribution functions in the presence of a stationary neutralising ion background. Beginning with the kinetic quantum plasma longitudinal susceptibility, we assess the effects due to increasing complexity of the background distribution function. Firstly, we analyse dispersion and Landau damping in one-component plasmas and consider distribution functions with a variety of analytical properties: the Dirac delta function, the Cauchy profile with two complex first-order poles, the squared Cauchy profile with two second-order poles and the inverse-quartic profile with four first-order poles; we also briefly discuss the non-meromorphic totally and arbitrarily degenerate Fermi–Dirac distribution. In order to study electrostatic instabilities, we then turn to plasmas with two populations of electrons streaming relative to each other in two cases: a symmetric case of two counter-streaming identical populations and a bump-on-tail case with a primary population and a delta-function beam. We obtain the corresponding linear kinetic dispersion relations and evaluate the properties of instabilities when the electron distribution functions are of the delta function, Cauchy, squared Cauchy or inverse-quartic types. In agreement with other studies, we find that in general quantum effects reduce the range of wavelengths for unstable modes at long wavelengths. We also find a second window of instability at shorter wavelengths and elucidate its nature as being due to quantum recoil. We note the possible implications for studies of laboratory and astrophysical quantum plasmas.

We compute the real and imaginary parts of the electric permittivities and magnetic permeabilities of relativistic electrons from quantum electrodynamics at finite temperatures and densities, for weak fields, neglecting electron–electron interactions. For non-zero temperatures, electromagnetic responses are reduced to one-dimensional integrals computed numerically. For zero temperature, we find analytic expressions for both their real/dispersive and imaginary/absorptive parts. As an application of our results, we obtain the dispersion relation for longitudinal electric plasmons. Present calculations support our recent claim that, at low frequencies and long wavelengths, the system will exhibit simultaneously negative electric and magnetic responses.

The acceleration of an electron by the ponderomotive force of a Gaussian whistler pulse in a magnetized high-density quantum plasma obeying Fermi–Dirac distribution is studied using the recently developed quantum hydrodynamic model. Effective acceleration takes place when the peak whistler amplitude exceeds a threshold value, and the whistler frequency is greater than the cyclotron frequency. The threshold amplitude decreases with ratio of plasma frequency to electron cyclotron frequency. The electron is accelerated at velocities of about twice the group velocity of the whistler.

The long-standing challenge to describing charged particle dynamics in strong classical electromagnetic fields is how to incorporate classical radiation, classical radiation reaction and quantized photon emission into a consistent unified framework. The current, semiclassical methods to describe the dynamics of quantum particles in strong classical fields also provide the theoretical framework for fundamental questions in gravity and hadron–hadron collisions, including Hawking radiation, cosmological particle production and thermalization of particles created in heavy-ion collisions. However, as we show, these methods break down for highly relativistic particles propagating in strong fields. They must therefore be improved and adapted for the description of laser–plasma experiments that typically involve the acceleration of electrons. Theory developed from quantum electrodynamics, together with dedicated experimental efforts, offer the best controllable context to establish a robust, experimentally validated foundation for the fundamental theory of quantum effects in strong classical potentials.

The possibilities of electron acceleration by ponderomotive force of a circularly polarized laser pulse in magnetized quantum plasma have been explored. The basic mechanism involves acceleration of electron by the axial gradient in the ponderomotive potential of the laser. The quantum effects have been taken into account for a high-density plasma. The ponderomotive force of the laser is resonantly enhanced when Doppler up-shifted laser frequency equals the cyclotron frequency.