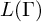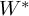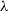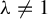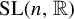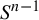3 results
Hyperbolic actions of higher rank lattices come from rank-one factors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 30 September 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We study actions of higher rank lattices
$\Gamma <G$ on hyperbolic spaces and we show that all such actions satisfying mild properties come from the rank-one factors of G. In particular, all non-elementary isometric actions on an unbounded hyperbolic space are of this type.
Orbit equivalence superrigidity for type III
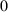$_0$ actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 4193-4225
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We prove the first orbit equivalence superrigidity results for actions of type III
$_\unicode{x3bb} $ when 
$\unicode{x3bb} \neq 1$. These actions arise as skew products of actions of dense subgroups of 
$\operatorname {SL}(n,\mathbb {R})$ on the sphere 
$S^{n-1}$ and they can have any prescribed associated flow.
Actions of higher-rank lattices on free groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 1573-1580
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
