A classical argument was introduced by Khintchine in 1926 in order to exhibit the existence of totally irrational singular linear forms in two variables. This argument was subsequently revisited and extended by many authors. For instance, in 1959 Jarník used it to show that for 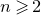 $n \geqslant 2$ and for any non-increasing positive f there are totally irrational matrices
$n \geqslant 2$ and for any non-increasing positive f there are totally irrational matrices 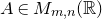 $A \in M_{m,n}(\mathbb{R})$ such that for all large enough t there are
$A \in M_{m,n}(\mathbb{R})$ such that for all large enough t there are 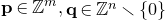 $\mathbf{p} \in \mathbb{Z}^m, \mathbf{q} \in \mathbb{Z}^n \smallsetminus \{0\}$ with
$\mathbf{p} \in \mathbb{Z}^m, \mathbf{q} \in \mathbb{Z}^n \smallsetminus \{0\}$ with 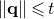 $\|\mathbf{q}\| \leqslant t$ and
$\|\mathbf{q}\| \leqslant t$ and 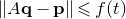 $\|A \mathbf{q} - \mathbf{p}\| \leqslant f(t)$. We denote the collection of such matrices by
$\|A \mathbf{q} - \mathbf{p}\| \leqslant f(t)$. We denote the collection of such matrices by 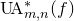 $\operatorname{UA}^*_{m,n}(f)$. We adapt Khintchine’s argument to show that the sets
$\operatorname{UA}^*_{m,n}(f)$. We adapt Khintchine’s argument to show that the sets 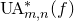 $\operatorname{UA}^*_{m,n}(f)$, and their weighted analogues
$\operatorname{UA}^*_{m,n}(f)$, and their weighted analogues 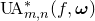 $\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$, intersect many manifolds and fractals, and have strong intersection properties. For example, we show that: (i) when
$\operatorname{UA}^*_{m,n}(f, {\boldsymbol{\omega}})$, intersect many manifolds and fractals, and have strong intersection properties. For example, we show that: (i) when 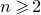 $n \geqslant 2$, the set
$n \geqslant 2$, the set 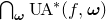 $\bigcap_{{\boldsymbol{\omega}}} \operatorname{UA}^*(f, {\boldsymbol{\omega}}) $, where the intersection is over all weights
$\bigcap_{{\boldsymbol{\omega}}} \operatorname{UA}^*(f, {\boldsymbol{\omega}}) $, where the intersection is over all weights  ${\boldsymbol{\omega}}$, is non-empty, and moreover intersects many manifolds and fractals; (ii) for
${\boldsymbol{\omega}}$, is non-empty, and moreover intersects many manifolds and fractals; (ii) for 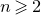 $n \geqslant 2$, there are vectors in
$n \geqslant 2$, there are vectors in 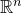 $\mathbb{R}^n$ which are simultaneously k-singular for every k, in the sense of Yu; and (iii) when
$\mathbb{R}^n$ which are simultaneously k-singular for every k, in the sense of Yu; and (iii) when 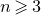 $n \geqslant 3$,
$n \geqslant 3$, 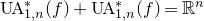 $\operatorname{UA}^*_{1,n}(f) + \operatorname{UA}^*_{1,n}(f) =\mathbb{R}^n$. We also obtain new bounds on the rate of singularity which can be attained by column vectors in analytic submanifolds of dimension at least 2 in
$\operatorname{UA}^*_{1,n}(f) + \operatorname{UA}^*_{1,n}(f) =\mathbb{R}^n$. We also obtain new bounds on the rate of singularity which can be attained by column vectors in analytic submanifolds of dimension at least 2 in 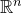 $\mathbb{R}^n$.
$\mathbb{R}^n$.
 $C^*$-algebras
$C^*$-algebras