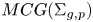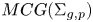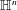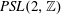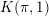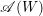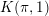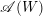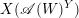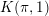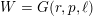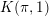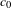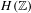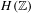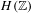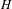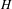Refine listing
Actions for selected content:
535 results in 20Fxx
GROUPS WITH NORMALITY CONDITIONS FOR UNCOUNTABLE SUBGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 268-277
- Print publication:
- October 2021
-
- Article
- Export citation
A combination theorem for combinatorially non-positively curved complexes of hyperbolic groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 445-477
- Print publication:
- May 2021
-
- Article
- Export citation
Simple groups and irreducible lattices in wreath products
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 07 February 2020, pp. 1502-1513
- Print publication:
- May 2021
-
- Article
- Export citation
Dehn filling Dehn twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 January 2020, pp. 28-51
- Print publication:
- February 2021
-
- Article
- Export citation
Ideal Uniform Polyhedra in
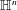 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 465-492
- Print publication:
- April 2021
-
- Article
- Export citation
On the
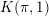 $K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
$K(\unicode[STIX]{x1D70B},1)$-problem for restrictions of complex reflection arrangements
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 3 / March 2020
- Published online by Cambridge University Press:
- 20 January 2020, pp. 526-532
- Print publication:
- March 2020
-
- Article
- Export citation
AXIOMATISABILITY OF THE CLASS OF MONOLITHIC GROUPS IN A VARIETY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 67-76
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Revisiting Leighton’s theorem with the Haar measure
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 615-623
- Print publication:
- May 2021
-
- Article
- Export citation
A NEW COARSELY RIGID CLASS OF BANACH SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 1729-1747
- Print publication:
- September 2021
-
- Article
- Export citation
ON FINITE-BY-NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 20 December 2019, pp. 54-58
- Print publication:
- January 2021
-
- Article
- Export citation
Higher generating subgroups and Cohen–Macaulay complexes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 17 December 2019, pp. 275-285
-
- Article
- Export citation
On commensurability of right-angled Artin groups II: RAAGs defined by paths
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 559-608
- Print publication:
- May 2021
-
- Article
- Export citation
Counting subgraphs in fftp graphs with symmetry
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 327-353
- Print publication:
- March 2021
-
- Article
- Export citation
Arithmeticity of the monodromy of some Kodaira fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 114-157
- Print publication:
- January 2020
-
- Article
- Export citation
Cube complexes and abelian subgroups of automorphism groups of RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 20 November 2019, pp. 523-547
- Print publication:
- May 2021
-
- Article
- Export citation
ALGEBRAIC ISOMONODROMIC DEFORMATIONS AND THE MAPPING CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 1497-1545
- Print publication:
- September 2021
-
- Article
- Export citation
Rigidity Properties for Hyperbolic Generalizations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 November 2019, pp. 66-76
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Maximal hyperbolic towers and weight in the theory of free groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 479-498
- Print publication:
- May 2021
-
- Article
- Export citation
Non-triviality of the Poisson boundary of random walks on the group
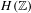 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 1160-1189
- Print publication:
- April 2021
-
- Article
- Export citation
GROUPS WHOSE NONNORMAL SUBGROUPS ARE METAHAMILTONIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 96-103
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation