 $n$
$n$
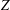 $Z$-EIGENPAIRS OF SYMMETRIC TENSORS
$Z$-EIGENPAIRS OF SYMMETRIC TENSORS
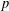 $p$-SUPERSOLUBILITY OF FINITE GROUPS
$p$-SUPERSOLUBILITY OF FINITE GROUPS
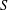 $S$-PERMUTABLY EMBEDDED SUBGROUPS OF FINITE GROUPS
$S$-PERMUTABLY EMBEDDED SUBGROUPS OF FINITE GROUPS