Research Article
A remark on a mean value theorem of Alexander Weinstein in Generalized Axially Symmetric Potential Theory
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-9
-
- Article
-
- You have access
- Export citation
Twisted group rings and a problem of Faith
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 11-19
-
- Article
-
- You have access
- Export citation
Extensions of a semilattice by an inverse semigroup
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 21-31
-
- Article
-
- You have access
- Export citation
Embedding near domains
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 33-42
-
- Article
-
- You have access
- Export citation
Finiteness conditions in soluble groups and Lie algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 43-48
-
- Article
-
- You have access
- Export citation
Conditions for a plane projective metric to be a norm
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 49-54
-
- Article
-
- You have access
- Export citation
Remark on a theorem of E.H. Brown
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 55-60
-
- Article
-
- You have access
- Export citation
On categorical semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 61-68
-
- Article
-
- You have access
- Export citation
The zero divisor question for supersolvable groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 69-71
-
- Article
-
- You have access
- Export citation
The algebra of functions with Fourier transforms in a given function space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 73-82
-
- Article
-
- You have access
- Export citation
Invariant metrics on free topological groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-88
-
- Article
-
- You have access
- Export citation
Quasi proximal continuity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 89-98
-
- Article
-
- You have access
- Export citation
A useful relationship in the conformal mapping of quadrilaterals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 99-104
-
- Article
-
- You have access
- Export citation
A generalization of a theorem of Aquaro
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 105-108
-
- Article
-
- You have access
- Export citation
Uniqueness of invariant means on certain introverted spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 109-120
-
- Article
-
- You have access
- Export citation
Uniqueness and representation of a function in terms of its translated averages
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 121-125
-
- Article
-
- You have access
- Export citation
Minimal generating sets for some wreath products of groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 127-136
-
- Article
-
- You have access
- Export citation
A final remark on extending to strict total orders in modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-140
-
- Article
-
- You have access
- Export citation
Matchings in graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 141-143
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
An algebraic approach to Runge-Kutta methods
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-146
-
- Article
-
- You have access
- Export citation

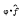 is Fourier transform of an
is Fourier transform of an 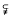
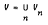 where each
where each