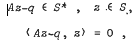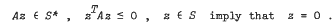Research Article
A note on generalised linear complementarity problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-168
-
- Article
-
- You have access
- Export citation
A structure theorem for operators with closed range
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-186
-
- Article
-
- You have access
- Export citation
Semi-simple classes in a variety satisfying an Andrunakievich Lemma
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 187-200
-
- Article
-
- You have access
- Export citation
Characterizations of MacNeille completions and topological functors
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 201-210
-
- Article
-
- You have access
- Export citation
Finite zero-simple semigroups over an elementary abelian group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-220
-
- Article
-
- You have access
- Export citation
Stein quasigroups I: Combinatorial aspects
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-236
-
- Article
-
- You have access
- Export citation
On boundedness of impulsively perturbed systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 237-242
-
- Article
-
- You have access
- Export citation
Resolving actions of compact Lie groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 243-254
-
- Article
-
- You have access
- Export citation
Periodic points and chaotic functions in the unit interval
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-265
-
- Article
-
- You have access
- Export citation
Measure theoretic techniques in topology and mappings of replete and measure replete spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-285
-
- Article
-
- You have access
- Export citation
The enumeration and bifurcations of ranking functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 287-292
-
- Article
-
- You have access
- Export citation
A counter-example to a conjecture by Deakin
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-294
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
The conformal group & Einstein spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 295-296
-
- Article
-
- You have access
- Export citation
Degree of approximation theorems for approximation with side conditions
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 297
-
- Article
-
- You have access
- Export citation
Some techniques of harmonic analysis on compact Lie groups with applications to lacunarity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-301
-
- Article
-
- You have access
- Export citation
Differentiable manifolds modelled on locally convex spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 303-304
-
- Article
-
- You have access
- Export citation
Maximal quotient rings of prime nonsingular group algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 305-306
-
- Article
-
- You have access
- Export citation
Radiation losses in dielectric optical waveguides
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-309
-
- Article
-
- You have access
- Export citation
Corrigendum
Martingale central limit theorems without uniform asymptotic negligibility: Corrigendum
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 311-319
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 18 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation