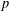 $p$-PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
$p$-PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
 $p$-SYLOW SUBGROUPS
$p$-SYLOW SUBGROUPS
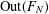 $\text{Out}(F_{N})$
$\text{Out}(F_{N})$
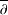 $\overline{\unicode[STIX]{x2202}}$-EQUATION IN DIRICHLET-TYPE SPACES
$\overline{\unicode[STIX]{x2202}}$-EQUATION IN DIRICHLET-TYPE SPACES
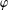 $\unicode[STIX]{x1D711}$-CONTRACTIBILITY AND
$\unicode[STIX]{x1D711}$-CONTRACTIBILITY AND 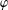 $\unicode[STIX]{x1D711}$-CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
$\unicode[STIX]{x1D711}$-CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
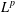 $L^{p}$-APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS
$L^{p}$-APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS