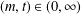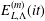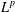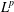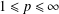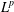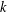Contents
Research Article
QUASICONFORMAL HARMONIC MAPPINGS BETWEEN DOMAINS CONTAINING INFINITY
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 109-117
-
- Article
-
- You have access
- Export citation
NOTE ON FOURIER–STIELTJES COEFFICIENTS OF COIN-TOSSING MEASURES
- Part of:
-
- Published online by Cambridge University Press:
- 20 April 2020, pp. 479-489
-
- Article
-
- You have access
- Export citation
SOLUTION BRANCHES OF NONLINEAR EIGENVALUE PROBLEMS ON RESTRICTED DOMAINS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2020, pp. 490-497
-
- Article
-
- You have access
- Export citation
ON A LATTICE GENERALISATION OF THE LOGARITHM AND A DEFORMATION OF THE DEDEKIND ETA FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2020, pp. 118-125
-
- Article
-
- You have access
- Open access
- Export citation
INEQUALITIES OF JENSEN’S TYPE FOR POSITIVE LINEAR FUNCTIONALS ON HERMITIAN UNITAL BANACH
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 308-318
-
- Article
-
- You have access
- Export citation
GRADIENT ESTIMATES VIA TWO-POINT FUNCTIONS FOR PARABOLIC EQUATIONS UNDER RICCI FLOW
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2020, pp. 319-330
-
- Article
-
- You have access
- Export citation
DEFORMING A STARSHAPED CURVE INTO A CIRCLE BY AN AREA-PRESERVING FLOW
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2020, pp. 498-505
-
- Article
-
- You have access
- Export citation
ON THE HYPERSTABILITY OF THE DRYGAS FUNCTIONAL EQUATION ON A RESTRICTED DOMAIN
-
- Published online by Cambridge University Press:
- 29 October 2019, pp. 126-137
-
- Article
-
- You have access
- Export citation
ON THE PROBLEM OF NON-BERWALDIAN LANDSBERG SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 331-341
-
- Article
-
- You have access
- Export citation
ARENS PRODUCTS, ARENS REGULARITY AND RELATED PROBLEMS
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2019, pp. 138-150
-
- Article
-
- You have access
- Export citation
SEQUENTIAL COLLISION-FREE OPTIMAL MOTION PLANNING ALGORITHMS IN PUNCTURED EUCLIDEAN SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2020, pp. 506-516
-
- Article
-
- You have access
- Export citation
COMPACT WEIGHTED COMPOSITION OPERATORS BETWEEN
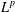 $L^{p}$-SPACES
$L^{p}$-SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2020, pp. 151-161
-
- Article
-
- You have access
- Export citation
AN IMPROVED LOWER BOUND FOR THE CRITICAL PARAMETER OF STAVSKAYA’S PROCESS
- Part of:
-
- Published online by Cambridge University Press:
- 13 May 2020, pp. 517-524
-
- Article
-
- You have access
- Export citation
ON THE
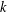 $k$-ERROR LINEAR COMPLEXITY OF SEQUENCES FROM FUNCTION FIELDS
$k$-ERROR LINEAR COMPLEXITY OF SEQUENCES FROM FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 342-352
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
BAZ volume 102 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 21 August 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
BAZ volume 102 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 November 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Retraction
ANCIENT SOLUTIONS OF CODIMENSION TWO SURFACES WITH CURVATURE PINCHING - RETRACTED
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2020, pp. 162-171
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
BAZ volume 102 Issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 21 August 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation
BAZ volume 102 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 November 2020, pp. b1-b6
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
ASSESSING HEALTHCARE PROVIDERS’ PERFORMANCE WITH AND WITHOUT RISK ADJUSTMENT
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2020, pp. 172-173
-
- Article
-
- You have access
- Export citation