It is shown that:

(i) a continuous function from a compact quasi-uniform space into a quasi-uniform space is not necessarily quasiuniformly continuous;

(ii) if the range of the function is a uniform space, the function will be necessarily quasi-uniformly continuous.

(This contradicts an example in the literature and generalizes a classical result.) Finally, a generalization of (ii) is given by means of a suitable boundedness notion.

Each metacyclic p–group has a natural canonical presentation which is easily derived from the usual presentation. Parameters in the canonical presentation measure how far the group is from splitting, and from being either commutative or dihedral. The structure of the groups is discussed.

In constructive mathematics the Dedekind cut definition of real number is not equivalent to the definition of real number by Cauchy sequences, and the Dedekind real numbers do not satisfy Heyting's axioms for constructive fields. A more general notion of constructive field is proposed which includes the Dedekind real numbers; some linear algebra is given which applies to such fields.

For a nonconstant L2 (−π, π) function f, we prove that and that the inequalities are sharp.

A condition which was previously found to be sufficient for global existence and uniqueness of solutions of an ordinary differential equation is shown herein to be necessary, if it is also required that solutions are exponentially bounded.

The purpose of this paper is to study the propagation of cylindrical shear waves in nonhomogeneous four-parameter viscoelastic plates of arbitrary thickness. The plates have a transverse cylindrical hole and their material properties are functions of the radial distance from the center of this opening. They are initially unstressed and at rest. A suddenly rising shearing traction is applied uniformly over the boundary of the opening and parallel to the faces of the plates and thereafter steadily maintained; they are otherwise free from loading. We consider both the case of a finite plate with a stress-free cylindrical outer boundary, and an infinite plate composed of two media in welded contact along a cylindrical surface symmetrical with respect to the center of the opening. We find that a reflected pulse is produced at the outer boundary of the finite plate while reflected and transmitted pulses are produced at the interface in the infinite bi-viscoelastic plate. Ray techniques are used throughout, and formal asymptotic wavefront expansions of the solution functions are obtained.

Chase has given several characterizations of a right coherent ring, among which are: every direct product of copies of the ring is left-flat; and every finitely generated submodule of a free right module is finitely related. We extend his results to obtain conditions for the ring of quotients of a ring with respect to a torsion theory to be coherent.

One problem in set theory without the axiom of choice is to find a reasonable way of estimating the size of a non-well-orderable set; in this paper we present evidence which suggests that this may be very hard. Given an arbitrary fixed aleph κ we construct a model of set theory which contains a set X such that if Y ⊆ X then either Y or X - Y is finite, but such that κ can be mapped into S(S(S(X))). So in one sense X is large and in another X is one of the smallest possible infinite sets. (Here S(X) is the power set of X.)

Let p be a prime and G a group with a p–reduced nilpotent normal subgroup N such that G/N is a nilpotent p–group. It is shown that if G has the subnormal intersection property and if G/N is finite or N is p–torsion-free, then G is nilpotent. This result is used to prove that an abelian-by-finite group has the subnormal intersection property if and only if it has a bound for the subnormal indices of its subnormal subgroups.

The existence of a certain type of Rudin-Shapiro sequence of functions is shown for all infinite compact groups which are not Lie, thus extending a recent result of the authors to all infinite compact groups.

As a special case of more general results, it is proved in this note that, if α is any real number and δ any positive number, then there exists a positive integer X such that the inequality

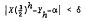
has infinitely many solutions in positive integers h and Yh.

The method depends on the study of infinite sequences of real linear forms in a fixed number of variables. It has relations to that used by Kronecker in the proof of his classical theorem and can be generalised.

This paper presents a theoretical investigation into the forced oscillations produced in an elongated lake by wind stresses varying in time. Analysis of the appropriate hydrodynamical equations of motion, in the absence of friction, and the equation of continuity give an estimate of the response function of the longitudinal component of the wind stress onto water level. Two mathematical models are used, one giving an analytical solution and the other requiring numerical methods for solution. The first model assumes that the lake is a homogeneous rectangular body of water and the second uses the mean depth h(x) and area of cross section A(x), considered as functions of distance x directed along the longitudinal axis of the lake.

We prove that if π is a generalized Hall plane of odd order with associated Baer subplane π0 then π is a Hall plane if and only if there is a collineation σ of π such that π0σ ∩ π0 is an affine point.

Let R be a ring of nonzero characteristic and let G be a finite group with subgroup H. It is shown that H is a normal subgroup of the group of units of the group ring RG if and only if H is contained in the centre of G or R is the field with 2 elements, G is the symmetric group on 3 letters and H is normal in G.

This paper shows the existence of a one-to-one correspondence between a certain class of square matrices of arbitrary order and a related extension field. The elements of these matrices are obtained from certain basic linear recursive sequences by means of a generalization of the euclidean algorithm.

The category of solid convergence spaces is introduced, and shown to lie strictly between the category of all convergence spaces and that of pseudo-topological spaces. A wide class of convergence spaces, including the c-embedded spaces of Binz, is then characterized in terms of this concept. Finally, several illustrative examples are given.

In this paper we present some approximation theorems for the eigenvalue problem of a compact linear operator defined on a Banach space. In particular we examine: criteria for the existence and convergence of approximate eigenvectors and generalized eigenvectors; relations between the dimensions of the eigenmanifolds and generalized eigenmanifolds of the operator and those of the approximate operators.

Carleson has proved that the Fourier series of functions belonging to the class L2 converge almost everywhere.

Improving his method, Hunt proved that the Fourier series of functions belonging to the class Lp (p > 1) converge almost everywhere. On the other hand, Kolmogoroff proved that there is an integrable function whose Fourier series diverges almost everywhere. We shall generalise Kolmogoroff's Theorem as follows: There is a function belonging to the class L(logL)p (p > 0) whose Fourier series diverges almost everywhere. The following problem is still open: whether “almost everywhere” in the last theorem can be replaced by “everywhere” or not. This problem is affirmatively answered for the class L by Kolmogoroff and for the class L(log logL)p (0 < p < 1) by Tandori.