We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove that neat and coneat submodules of a module coincide when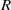 
$R$ is a commutative ring such that every maximal ideal is principal, extending a recent result by Fuchs. We characterise absolutely neat (coneat) modules and study their closure properties. We show that a module is absolutely neat if and only if it is injective with respect to the Dickson torsion theory.
$s$-GEODESIC TRANSITIVE GRAPHS