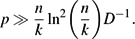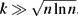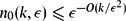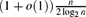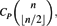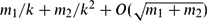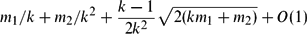Contents
Paper
Saturated Graphs of Prescribed Minimum Degree
-
- Published online by Cambridge University Press:
- 07 December 2016, pp. 201-207
-
- Article
- Export citation
Generalized Majority Colourings of Digraphs
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2017, pp. 850-855
-
- Article
- Export citation
Bridge-Addability, Edge-Expansion and Connectivity
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2017, pp. 697-719
-
- Article
- Export citation
Erdős–Ko–Rado for Random Hypergraphs: Asymptotics and Stability
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 406-422
-
- Article
- Export citation
Large Unavoidable Subtournaments
- Part of:
-
- Published online by Cambridge University Press:
- 21 June 2016, pp. 68-77
-
- Article
- Export citation
The Threshold Probability for Long Cycles
- Part of:
-
- Published online by Cambridge University Press:
- 08 September 2016, pp. 208-247
-
- Article
- Export citation
Minimum Codegree Threshold for C 6 3-Factors in 3-Uniform Hypergraphs
-
- Published online by Cambridge University Press:
- 22 March 2017, pp. 536-559
-
- Article
- Export citation
Local Conditions for Exponentially Many Subdivisions
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2016, pp. 423-430
-
- Article
- Export citation
Sets in Almost General Position
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2017, pp. 720-745
-
- Article
- Export citation
Exact Minimum Codegree Threshold for K − 4-Factors
-
- Published online by Cambridge University Press:
- 04 August 2017, pp. 856-885
-
- Article
- Export citation
On the Number of 4-Edge Paths in Graphs With Given Edge Density
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2016, pp. 431-447
-
- Article
- Export citation
The Structure of Typical Eye-Free Graphs and a Turán-Type Result for Two Weighted Colours
-
- Published online by Cambridge University Press:
- 31 July 2017, pp. 886-910
-
- Article
- Export citation
On the Chromatic Number of Random Cayley Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2016, pp. 248-266
-
- Article
- Export citation
Saturation in the Hypercube and Bootstrap Percolation
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2016, pp. 78-98
-
- Article
- Export citation
Simply Generated Non-Crossing Partitions
-
- Published online by Cambridge University Press:
- 28 March 2017, pp. 560-592
-
- Article
- Export citation
Mixing in High-Dimensional Expanders
-
- Published online by Cambridge University Press:
- 17 May 2017, pp. 746-761
-
- Article
- Export citation
Forbidden Hypermatrices Imply General Bounds on Induced Forbidden Subposet Problems
-
- Published online by Cambridge University Press:
- 15 February 2017, pp. 593-602
-
- Article
- Export citation
Distinct Distances on Algebraic Curves in the Plane
-
- Published online by Cambridge University Press:
- 15 July 2016, pp. 99-117
-
- Article
- Export citation
Fractional Clique Decompositions of Dense Partite Graphs
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2017, pp. 911-943
-
- Article
- Export citation
Judicious Partitioning of Hypergraphs with Edges of Size at Most 2†
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2016, pp. 267-284
-
- Article
- Export citation