Contents
Research Article
Minimization Problems for Infinite n-Connected Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 417-436
-
- Article
- Export citation
Optimally Reliable Graphs for Both Vertex and Edge Failures
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 93-100
-
- Article
- Export citation
Random Matrices and Brownian Motion†
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 157-180
-
- Article
- Export citation
A Mildly Exponential Time Algorithm for Approximating the Number of Solutions to a Multidimensional Knapsack Problem
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 271-284
-
- Article
- Export citation
Factorization in Fq[x] and Brownian Motion
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 285-299
-
- Article
- Export citation
Front matter
CPC volume 2 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Image Partition Regularity of Matrices
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 437-463
-
- Article
- Export citation
A Discrete Analogue of a Theorem of Makarov
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 181-199
-
- Article
- Export citation
Geometric Approaches to the Estimation of the Spectral Gap of Reversible Markov Chains
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 301-323
-
- Article
- Export citation
Back matter
CPC volume 2 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, p. b1
-
- Article
-
- You have access
- Export citation
Research Article
Extremal Graph Problems for Graphs with a Color-Critical Vertex
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 465-477
-
- Article
- Export citation
Linear-Time Approximation Algorithms for the Max Cut Problem
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 201-210
-
- Article
- Export citation
A Zero-Free Interval for Chromatic Polynomials of Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 325-336
-
- Article
- Export citation
Triangle-Free Graphs with High Minimal Degrees
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 479-490
-
- Article
- Export citation
Front matter
CPC volume 2 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Local-Global Phenomena in Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 491-503
-
- Article
- Export citation
Threshold Channel Graphs
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 337-349
-
- Article
- Export citation
Back matter
CPC volume 2 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
On Random Generation of the Symmetric Group
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 505-512
-
- Article
- Export citation
Threshold Functions for Markov Chains: a Graph Theoretic Approach
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 351-362
-
- Article
- Export citation
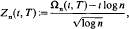
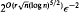 time randomized algorithm that estimates the number of feasible solutions of a multidimensional knapsack problem within 1 ±
time randomized algorithm that estimates the number of feasible solutions of a multidimensional knapsack problem within 1 ±