Refine listing
Actions for selected content:
Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 18
UNIFORM ASYMPTOTIC NORMALITY IN STATIONARY AND UNIT ROOT AUTOREGRESSION
-
- Published online by Cambridge University Press:
- 14 April 2011, pp. 1117-1151
-
- Article
- Export citation
- Cited by 18
CONVERGENCE RATES FOR ILL-POSED INVERSE PROBLEMS WITH AN UNKNOWN OPERATOR
-
- Published online by Cambridge University Press:
- 11 October 2010, pp. 522-545
-
- Article
- Export citation
- Cited by 18
THE BOOTSTRAP IN THRESHOLD REGRESSION
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. 676-714
-
- Article
- Export citation
- Cited by 18
The Limit Distribution of level Crossings of a Random Walk, and a Simple Unit Root Test
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 705-723
-
- Article
- Export citation
- Cited by 17
THE ET INTERVIEW: PROFESSOR DAVID F. HENDRY: Interviewed by Neil R. Ericsson
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2004, pp. 743-804
-
- Article
- Export citation
- Cited by 17
On the Sensitivity of a Regression Coefficient to Monotonic Transformations
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 165-169
-
- Article
- Export citation
- Cited by 17
Asymptotic Normmality of Maximum Likelihood Estimators Obtained from Normally Distributed but Dependent Observations
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 374-412
-
- Article
- Export citation
- Cited by 17
A Theory of Serial Correlation of Stochastic Taste Changers in Direct Utility Functions
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 192-210
-
- Article
- Export citation
- Cited by 17
The VPRT: A Sequential Testing Procedure Dominating the SPRT
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 431-450
-
- Article
- Export citation
- Cited by 17
THE GLOBAL WEIGHTED LAD ESTIMATORS FOR FINITE/INFINITE VARIANCE ARMA(p,q) MODELS
-
- Published online by Cambridge University Press:
- 27 April 2012, pp. 1065-1086
-
- Article
- Export citation
- Cited by 17
TESTING FOR LONG MEMORY
-
- Published online by Cambridge University Press:
- 06 September 2007, pp. 143-175
-
- Article
- Export citation
- Cited by 17
Estimation of Cointegration Vectors with Linear Restrictions
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 19-35
-
- Article
- Export citation
- Cited by 17
An Exact Discrete Analog to a Closed LinearFirst-Order Continuous-Time System with MixedSample
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 143-149
-
- Article
- Export citation
- Cited by 17
ESTIMATION AND INFERENCE WITH NEAR UNIT ROOTS
-
- Published online by Cambridge University Press:
- 27 July 2022, pp. 221-263
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 17
NONPARAMETRIC TWO-STEP SIEVE M ESTIMATION AND INFERENCE
-
- Published online by Cambridge University Press:
- 25 April 2018, pp. 1281-1324
-
- Article
- Export citation
- Cited by 17
Classes of Similar Regions and Their PowerProperties for Some Econometric TestingProblems
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 1-44
-
- Article
- Export citation
- Cited by 17
DECIDING BETWEEN I(0) AND I(1) VIA FLIL-BASED BOUNDS
-
- Published online by Cambridge University Press:
- 01 October 1999, pp. 643-663
-
- Article
- Export citation
- Cited by 17
PARTIALLY SUPERFLUOUS OBSERVATIONS
-
- Published online by Cambridge University Press:
- 15 March 2006, pp. 529-536
-
- Article
- Export citation
- Cited by 17
ON THE BIMODALITY OF THE EXACT DISTRIBUTION OF THE TSLS ESTIMATOR
-
- Published online by Cambridge University Press:
- 30 August 2006, pp. 932-946
-
- Article
- Export citation
- Cited by 17
THE ASYMPTOTIC EFFICIENCY OF COINTEGRATION ESTIMATORS UNDER TEMPORAL AGGREGATION
-
- Published online by Cambridge University Press:
- 08 January 2003, pp. 49-77
-
- Article
- Export citation
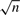 when
when 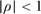 and the limit distribution is the same as the Gaussian maximum likelihood estimator (MLE), but when
and the limit distribution is the same as the Gaussian maximum likelihood estimator (MLE), but when 