Refine listing
Actions for selected content:
Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 5
NONSTATIONARY LINEAR PROCESSES WITH INFINITE VARIANCE GARCH ERRORS
-
- Published online by Cambridge University Press:
- 26 October 2020, pp. 892-925
-
- Article
- Export citation
- Cited by 5
THE IMPACT OF PERSISTENT CYCLES ON ZERO FREQUENCY UNIT ROOT TESTS
-
- Published online by Cambridge University Press:
- 20 August 2013, pp. 1289-1313
-
- Article
- Export citation
- Cited by 5
THE PROPERTIES OF KULLBACK–LEIBLER DIVERGENCE FOR THE UNIT ROOT HYPOTHESIS
-
- Published online by Cambridge University Press:
- 01 December 2009, pp. 1662-1681
-
- Article
- Export citation
- Cited by 5
ESTIMATION OF A SEMIPARAMETRIC IGARCH(1,1) MODEL
-
- Published online by Cambridge University Press:
- 04 November 2010, pp. 639-661
-
- Article
- Export citation
- Cited by 5
SEMIPARAMETRIC ESTIMATION OF RANDOM COEFFICIENTS IN STRUCTURAL ECONOMIC MODELS
-
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1265-1305
-
- Article
- Export citation
- Cited by 5
Testing Linear Restrictions with Unequal Variances
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 349
-
- Article
- Export citation
- Cited by 5
The Bias of the Standard Errors of OLS for an AR(1) Process with an Arbitrary Variance on the Initial Observations
-
- Published online by Cambridge University Press:
- 18 October 2010, p. 146
-
- Article
- Export citation
- Cited by 5
Effect of an Additional Regressor on R2
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 441-442
-
- Article
- Export citation
- Cited by 5
COMPLETE SUBSET AVERAGING FOR QUANTILE REGRESSIONS
-
- Published online by Cambridge University Press:
- 13 August 2021, pp. 146-188
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 5
FACTORISABLE MULTITASK QUANTILE REGRESSION
-
- Published online by Cambridge University Press:
- 22 September 2020, pp. 794-816
-
- Article
- Export citation
- Cited by 5
The Distribution of the Stein-Rule Estimator in a Model with Non-Normal Disturbances
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 202-219
-
- Article
- Export citation
- Cited by 5
03.6.1 The Central Limit Theorem for Student's Distribution—Solution
-
- Published online by Cambridge University Press:
- 01 December 2004, pp. 1261-1263
-
- Article
- Export citation
- Cited by 5
A Hausman Specification Test in a Simultaneous Equations Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 537-538
-
- Article
- Export citation
- Cited by 5
THE LOCAL ASYMPTOTIC POWER OF CERTAIN TESTS FOR FRACTIONAL INTEGRATION
-
- Published online by Cambridge University Press:
- 01 October 1999, pp. 704-709
-
- Article
- Export citation
- Cited by 5
TEST FOR ZERO MEDIAN OF ERRORS IN AN ARMA–GARCH MODEL
-
- Published online by Cambridge University Press:
- 09 June 2021, pp. 536-561
-
- Article
- Export citation
- Cited by 5
Professor H.O.A. Wold:1908–1992
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 419-433
-
- Article
- Export citation
- Cited by 5
ADAPTIVE NONPARAMETRIC REGRESSION WITH CONDITIONAL HETEROSKEDASTICITY
-
- Published online by Cambridge University Press:
- 08 September 2014, pp. 1153-1191
-
- Article
- Export citation
- Cited by 5
03.2.1. Fixed Effects Estimation of the Population-Averaged Slopes in a Panel Data Random Coefficient Model
-
- Published online by Cambridge University Press:
- 01 April 2003, pp. 411-412
-
- Article
- Export citation
- Cited by 5
ESTIMATION OF DIFFERENTIAL-DIFFERENCE EQUATION SYSTEMS WITH UNKNOWN LAG PARAMETERS
-
- Published online by Cambridge University Press:
- 15 March 2006, pp. 483-498
-
- Article
- Export citation
- Cited by 5
OPTIMAL BANDWIDTH CHOICE FOR ESTIMATION OF INVERSE CONDITIONAL–DENSITY–WEIGHTED EXPECTATIONS
-
- Published online by Cambridge University Press:
- 19 June 2009, pp. 94-118
-
- Article
- Export citation

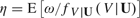 , where the conditional density of a scalar continuous random variable
, where the conditional density of a scalar continuous random variable 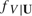 , is replaced by its kernel estimator. That is, the parameter
, is replaced by its kernel estimator. That is, the parameter 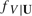 , and it is the building block of various semiparametric estimators already proposed in the literature such as Lewbel (1998), Lewbel (2000b), Honoré and Lewbel (2002), Khan and Lewbel (2007), and Lewbel (2007). The optimal bandwidth is derived by minimizing the leading terms of a second-order mean squared error expansion of an in-probability approximation of the resulting estimator with respect to
, and it is the building block of various semiparametric estimators already proposed in the literature such as Lewbel (1998), Lewbel (2000b), Honoré and Lewbel (2002), Khan and Lewbel (2007), and Lewbel (2007). The optimal bandwidth is derived by minimizing the leading terms of a second-order mean squared error expansion of an in-probability approximation of the resulting estimator with respect to 