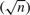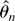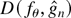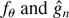Refine listing
Actions for selected content:
Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 5
VISION AND INFLUENCE IN ECONOMETRICS: JOHN DENIS SARGAN
-
- Published online by Cambridge University Press:
- 20 March 2003, pp. 495-511
-
- Article
- Export citation
- Cited by 5
ON THE ASYMPTOTIC PROPERTIES OF SOME SEASONAL UNIT ROOT TESTS
-
- Published online by Cambridge University Press:
- 31 January 2003, pp. 311-321
-
- Article
- Export citation
- Cited by 5
TESTING THE ORDER OF FRACTIONAL INTEGRATION OF A TIME SERIES IN THE POSSIBLE PRESENCE OF A TREND BREAK AT AN UNKNOWN POINT
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 1201-1233
-
- Article
- Export citation
- Cited by 5
A GENERALIZATION OF THE BURRIDGE–GUERRE NONPARAMETRIC UNIT ROOT TEST
-
- Published online by Cambridge University Press:
- 23 May 2006, pp. 756-761
-
- Article
- Export citation
- Cited by 5
Calculating the Distribution of the Serial Correlation Estimator by Saddlepoint Integration
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 458-480
-
- Article
- Export citation
- Cited by 5
Asymptotically Optimal Tests Using Limited Information and Testing for Exogeneity
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 53-69
-
- Article
- Export citation
- Cited by 5
Estimation of a Triangular, Seemingly Unrelated, Regression System by OLS
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 463
-
- Article
- Export citation
- Cited by 5
Equivariance of an Instrumental Variable (IV) Estimator in the Linear Regression Model
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 464
-
- Article
- Export citation
- Cited by 5
Prediction with a Two-Way Error Component Regression Model
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 175-177
-
- Article
- Export citation
- Cited by 5
Differentiation of an Exponential Matrix Function
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 1182-1185
-
- Article
- Export citation
- Cited by 4
STATIONARY INTEGRATED ARCH(∞) AND AR(∞) PROCESSES WITH FINITE VARIANCE
-
- Published online by Cambridge University Press:
- 17 October 2017, pp. 1159-1179
-
- Article
- Export citation
- Cited by 4
EFFICIENT ESTIMATION OF INTEGRATED VOLATILITY FUNCTIONALS UNDER GENERAL VOLATILITY DYNAMICS
-
- Published online by Cambridge University Press:
- 17 July 2020, pp. 664-707
-
- Article
- Export citation
- Cited by 4
LOCAL COMPOSITE QUANTILE REGRESSION SMOOTHING: A FLEXIBLE DATA STRUCTURE AND CROSS-VALIDATION
-
- Published online by Cambridge University Press:
- 26 March 2020, pp. 613-631
-
- Article
- Export citation
- Cited by 4
LET’S GET LADE: ROBUST ESTIMATION OF SEMIPARAMETRIC MULTIPLICATIVE VOLATILITY MODELS
-
- Published online by Cambridge University Press:
- 05 November 2014, pp. 671-702
-
- Article
- Export citation
- Cited by 4
TWO-STEP ESTIMATION OF QUANTILE PANEL DATA MODELS WITH INTERACTIVE FIXED EFFECTS
-
- Published online by Cambridge University Press:
- 18 August 2022, pp. 419-446
-
- Article
- Export citation
- Cited by 4
PARAMETRIC SPECIFICATION TEST FOR NONLINEAR AUTOREGRESSIVE MODELS
-
- Published online by Cambridge University Press:
- 02 October 2014, pp. 1078-1101
-
- Article
- Export citation
- Cited by 4
HIGHER ORDER ASYMPTOTIC THEORY FOR MINIMUM CONTRAST ESTIMATORS OF SPECTRAL PARAMETERS OF STATIONARY PROCESSES
-
- Published online by Cambridge University Press:
- 24 September 2003, pp. 984-1007
-
- Article
- Export citation
- Cited by 4
OPTIMAL VERSUS ROBUST INFERENCE IN NEARLY INTEGRATED NON-GAUSSIAN MODELS
-
- Published online by Cambridge University Press:
- 05 March 2004, pp. 23-55
-
- Article
- Export citation
- Cited by 4
REX BERGSTROM’S CONTRIBUTIONS TO CONTINUOUS TIME MACROECONOMETRIC MODELING
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1087-1098
-
- Article
- Export citation
- Cited by 4
FINITE-SAMPLE SIZE CONTROL OF IVX-BASED TESTS IN PREDICTIVE REGRESSIONS
-
- Published online by Cambridge University Press:
- 10 August 2020, pp. 769-793
-
- Article
-
- You have access
- Open access
- Export citation