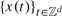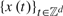Refine listing
Actions for selected content:
Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 2
APERIODIC DYNAMICS IN THE BERGSTROM/WYMER MODEL OF THE UNITED KINGDOM
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1099-1111
-
- Article
- Export citation
- Cited by 2
TESTING FOR STRICT STATIONARITY VIA THE DISCRETE FOURIER TRANSFORM
-
- Published online by Cambridge University Press:
- 28 October 2022, pp. 511-557
-
- Article
- Export citation
- Cited by 2
LAD ASYMPTOTICS UNDER CONDITIONALHETEROSKEDASTICITY WITH POSSIBLY INFINITE ERRORDENSITIES
-
- Published online by Cambridge University Press:
- 05 March 2010, pp. 953-962
-
- Article
- Export citation
- Cited by 2
CONTINUOUSLY UPDATED INDIRECT INFERENCE IN HETEROSKEDASTIC SPATIAL MODELS
-
- Published online by Cambridge University Press:
- 22 September 2021, pp. 107-145
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 2
Generalized Inverses of Partitioned Matrices
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 426-427
-
- Article
- Export citation
- Cited by 2
LINEAR NONSTATIONARY MODELS—A REVIEW OF THE WORK OF PROFESSOR P.C.B. PHILLIPS
-
- Published online by Cambridge University Press:
- 10 March 2014, pp. 815-838
-
- Article
- Export citation
- Cited by 2
SPECIFICATION TESTS FOR LATTICE PROCESSES
-
- Published online by Cambridge University Press:
- 19 August 2014, pp. 294-336
-
- Article
- Export citation
- Cited by 2
POST-SELECTION INFERENCE IN THREE-DIMENSIONAL PANEL DATA
-
- Published online by Cambridge University Press:
- 15 March 2022, pp. 623-658
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 2
VALID HETEROSKEDASTICITY ROBUST TESTING
-
- Published online by Cambridge University Press:
- 11 September 2023, pp. 249-301
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 2
ON MULTIPLE STRUCTURAL BREAKS IN DISTRIBUTION: AN EMPIRICAL CHARACTERISTIC FUNCTION APPROACH
-
- Published online by Cambridge University Press:
- 25 March 2022, pp. 534-581
-
- Article
- Export citation
- Cited by 2
UNIT ROOTS IN LIFE—A GRADUATE STUDENT STORY
-
- Published online by Cambridge University Press:
- 25 February 2014, pp. 719-736
-
- Article
- Export citation
- Cited by 2
A Note on Asymptotic Power Calculations in Nearly Nonstationary Time Series
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 659-667
-
- Article
- Export citation
- Cited by 2
Spurious Regression and Generalized Least Squares
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 967-968
-
- Article
- Export citation
- Cited by 2
STRUCTURAL CHANGES AND SEEMINGLY UNIDENTIFIED STRUCTURAL EQUATIONS
-
- Published online by Cambridge University Press:
- 15 May 2002, pp. 744-775
-
- Article
- Export citation
- Cited by 2
03.3.2. The Asymptotic Distribution of the Dickey–Fuller Statistic under Nonnegativity Constraint—Solution
-
- Published online by Cambridge University Press:
- 01 August 2004, pp. 808-810
-
- Article
- Export citation
- Cited by 2
EFFICIENT METHOD OF MOMENTS IN MISSPECIFIED I.I.D. MODELS
-
- Published online by Cambridge University Press:
- 08 June 2004, pp. 513-534
-
- Article
- Export citation
- Cited by 2
Moore-Penrose Inverse of a Matrix Product with Normal Matrix
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 653-654
-
- Article
- Export citation
- Cited by 2
A Matrix Equality Applicable in the Analysis of Mean-and-Covariance Structures
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 581-582
-
- Article
- Export citation
- Cited by 2
ECT volume 26 issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 September 2010, pp. b1-b4
-
- Article
-
- You have access
- Export citation
- Cited by 2
Eigenvalues of the Product of NonnegativeDefinite Matrices
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 808
-
- Article
- Export citation