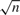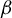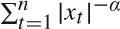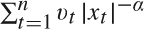Refine listing
Actions for selected content:
Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
Contents
- Cited by 2
Spurious Regression in Forecast-Encompassing Tests
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 1188-1190
-
- Article
- Export citation
- Cited by 2
THE ET INTERVIEW: PROFESSOR W. ERWIN DIEWERT
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2017, pp. 509-542
-
- Article
- Export citation
- Cited by 2
A Comparison of Ordinary Least Squares and Least Absolute Error Estimation
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 517-527
-
- Article
- Export citation
- Cited by 2
BOOTSTRAP ASSISTED SPECIFICATION TESTS FOR THE ARFIMA MODEL
-
- Published online by Cambridge University Press:
- 14 April 2011, pp. 1083-1116
-
- Article
- Export citation
- Cited by 2
An Inequality Concerning the Hadamard Matrix Product
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 464
-
- Article
- Export citation
- Cited by 2
SMOOTHED QUANTILE REGRESSION PROCESSES FOR BINARY RESPONSE MODELS
-
- Published online by Cambridge University Press:
- 20 May 2019, pp. 292-330
-
- Article
- Export citation
- Cited by 2
ON SMOOTH TESTS FOR THE EQUALITY OF DISTRIBUTIONS
-
- Published online by Cambridge University Press:
- 12 January 2021, pp. 194-208
-
- Article
- Export citation
- Cited by 2
The Asymptotic Local Structure of the Cox Modified Likelihood-Ratio Statistic for Testing Non-Nested Hypotheses
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 553-569
-
- Article
- Export citation
- Cited by 2
LIMIT LAWS IN TRANSACTION-LEVEL ASSET PRICE MODELS
-
- Published online by Cambridge University Press:
- 18 November 2013, pp. 536-579
-
- Article
- Export citation
- Cited by 2
NONPARAMETRIC ESTIMATION OF GENERALIZED TRANSFORMATION MODELS WITH FIXED EFFECTS
-
- Published online by Cambridge University Press:
- 20 January 2022, pp. 357-388
-
- Article
- Export citation
- Cited by 2
ALMOST SURE BOUNDS ON THE ESTIMATION ERROR FOR OLS ESTIMATORS WHEN THE REGRESSORS INCLUDE CERTAIN MFI(1) PROCESSES
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 571-582
-
- Article
- Export citation
- Cited by 2
Stochastic Limit Theory: An Introduction for EconometriciansJames Davidson, Oxford University Press, 1994
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 859-865
-
- Article
- Export citation
- Cited by 2
ANOTHER NUMERICAL METHOD OF FINDINGCRITICAL VALUES FOR THE ANDREWS STABILITYTEST
-
- Published online by Cambridge University Press:
- 02 August 2011, pp. 239-246
-
- Article
- Export citation
- Cited by 2
An Inequality for the Block-PartitionedInverse
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 543
-
- Article
- Export citation
- Cited by 2
DIFFERENCING TRANSFORMATIONS AND INFERENCE IN PREDICTIVE REGRESSION MODELS
-
- Published online by Cambridge University Press:
- 09 October 2014, pp. 1331-1358
-
- Article
- Export citation
- Cited by 2
SUBGEOMETRICALLY ERGODIC AUTOREGRESSIONS
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 959-985
-
- Article
- Export citation
- Cited by 2
A Class of Bivariate Density Functions with Common Marginals
-
- Published online by Cambridge University Press:
- 18 October 2010, pp. 145-146
-
- Article
- Export citation
- Cited by 2
ON THE ORDER OF MAGNITUDE OF SUMS OF NEGATIVE POWERS OF INTEGRATED PROCESSES
-
- Published online by Cambridge University Press:
- 12 November 2012, pp. 642-658
-
- Article
- Export citation
- Cited by 2
A NONPARAMETRIC TEST OF HETEROGENEITY IN CONDITIONAL QUANTILE TREATMENT EFFECTS
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 660-687
-
- Article
-
- You have access
- Open access
- Export citation
- Cited by 2
A SIMPLE NONPARAMETRIC APPROACH FOR ESTIMATION AND INFERENCE OF CONDITIONAL QUANTILE FUNCTIONS
-
- Published online by Cambridge University Press:
- 13 December 2021, pp. 290-320
-
- Article
-
- You have access
- Open access
- Export citation
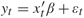 ,
, 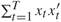 tends to infinity (a.s.) and log(
tends to infinity (a.s.) and log(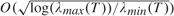 . In this note
. In this note