For long memory time series models with uncorrelated but dependent errors, we establish the asymptotic normality of the Whittle estimator under mild conditions. Our framework includes the widely used fractional autoregressive integrated moving average models with generalized autoregressive conditional heteroskedastic-type innovations. To cover nonstationary fractionally integrated processes, we extend the idea of Abadir, Distaso, and Giraitis (2007, Journal of Econometrics 141, 1353–1384) and develop the nonstationarity-extended Whittle estimation. The resulting estimator is shown to be asymptotically normal and is more efficient than the tapered Whittle estimator. Finally, the results from a small simulation study are presented to corroborate our theoretical findings.

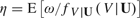This paper characterizes the bandwidth value (h) that is optimal for estimating parameters of the form , where the conditional density of a scalar continuous random variable 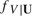V, given a random vector U, , is replaced by its kernel estimator. That is, the parameter 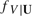η is the expectation of ω inversely weighted by , and it is the building block of various semiparametric estimators already proposed in the literature such as Lewbel (1998), Lewbel (2000b), Honoré and Lewbel (2002), Khan and Lewbel (2007), and Lewbel (2007). The optimal bandwidth is derived by minimizing the leading terms of a second-order mean squared error expansion of an in-probability approximation of the resulting estimator with respect to h. The expansion also demonstrates that the bandwidth can be chosen on the basis of bias alone, and that a simple “plug-in” estimator for the optimal bandwidth can be constructed. Finally, the small sample performance of our proposed estimator of the optimal bandwidth is assessed by a Monte Carlo experiment.

We derive the semiparametric efficiency bound in dynamic models of conditional quantiles under a sole strong mixing assumption. We also provide an expression of Stein’s (1956) least favorable parametric submodel. Our approach is as follows: First, we construct a fully parametric submodel of the semiparametric model defined by the conditional quantile restriction that contains the data generating process. We then compare the asymptotic covariance matrix of the MLE obtained in this submodel with those of the M-estimators for the conditional quantile parameter that are consistent and asymptotically normal. Finally, we show that the minimum asymptotic covariance matrix of this class of M-estimators equals the asymptotic covariance matrix of the parametric submodel MLE. Thus, (i) this parametric submodel is a least favorable one, and (ii) the expression of the semiparametric efficiency bound for the conditional quantile parameter follows.

This article investigates model checks for a class of possibly nonlinear heteroskedastic time series models, including but not restricted to ARMA-GARCH models. We propose omnibus tests based on functionals of certain weighted standardized residual empirical processes. The new tests are asymptotically distribution-free, suitable when the conditioning set is infinite-dimensional, and consistent against a class of Pitman’s local alternatives converging at the parametric rate n−1/2, with n the sample size. A Monte Carlo study shows that the simulated level of the proposed tests is close to the asymptotic level already for moderate sample sizes and that tests have a satisfactory power performance. Finally, we illustrate our methodology with an application to the well-known S&P 500 daily stock index. The paper also contains an asymptotic uniform expansion for weighted residual empirical processes when initial conditions are considered, a result of independent interest.

An effective way to control for cross-section correlation when conducting a panel unit root test is to remove the common factors from the data. However, there remain many ways to use the defactored residuals to construct a test. In this paper, we use the panel analysis of nonstationarity in idiosyncratic and common components (PANIC) residuals to form two new tests. One estimates the pooled autoregressive coefficient, and one simply uses a sample moment. We establish their large-sample properties using a joint limit theory. We find that when the pooled autoregressive root is estimated using data detrended by least squares, the tests have no power. This result holds regardless of how the data are defactored. All PANIC-based pooled tests have nontrivial power because of the way the linear trend is removed.

The paper discusses contemporaneous aggregation of the Linear ARCH (LARCH) model as defined in (1), which was introduced in Robinson (1991) and studied in Giraitis, Robinson, and Surgailis (2000) and other works. We show that the limiting aggregate of the (G)eneralized LARCH(1,1) process in (3)–(4) with random Beta distributed coefficient β exhibits long memory. In particular, we prove that squares of the limiting aggregated process have slowly decaying correlations and their partial sums converge to a self-similar process of a new type.

Semiparametric methods are widely employed in applied work where the ability to conduct inferences is important. To establish asymptotic normality for making inferences, bias control mechanisms are often used in implementing semiparametric estimators. The first contribution of this paper is to propose a mechanism that enables us to establish asymptotic normality with regular kernels. In so doing, we argue that the resulting estimator performs very well in finite samples.

Semiparametric models are commonly estimated under a single index assumption. Because the consistency of the estimator critically depends on this assumption being correct, our second objective is to develop a test for it. To ensure that the test statistic has good size and power properties in finite samples, we employ a bias control mechanism similar to that underlying the estimator. Furthermore, we structure the test so that its form adapts to the model under the alternative hypothesis. Monte Carlo results confirm that the bias control and the adaptive feature significantly improve the performance of the test statistic in finite samples.

This paper develops new estimation and inference procedures for dynamic panel data models with fixed effects and incidental trends. A simple consistent GMM estimation method is proposed that avoids the weak moment condition problem that is known to affect conventional GMM estimation when the autoregressive coefficient (ρ) is near unity. In both panel and time series cases, the estimator has standard Gaussian asymptotics for all values of ρ ∈ (−1, 1] irrespective of how the composite cross-section and time series sample sizes pass to infinity. Simulations reveal that the estimator has little bias even in very small samples. The approach is applied to panel unit root testing.

In this paper we analyze the asymptotic properties of the popular distribution tail index estimator by Hill (1975) for dependent, heterogeneous processes. We develop new extremal dependence measures that characterize a massive array of linear, nonlinear, and conditional volatility processes with long or short memory. We prove that the Hill estimator is weakly and uniformly weakly consistent for processes with extremes that form mixingale sequences and asymptotically normal for processes with extremes that are near epoch dependent (NED) on some arbitrary mixing functional. The extremal persistence assumptions in this paper are known to hold for mixing, Lp-NED, and some non-Lp-NED processes, including ARFIMA, FIGARCH, explosive GARCH, nonlinear ARMA-GARCH, and bilinear processes, and nonlinear distributed lags like random coefficient and regime-switching autoregressions.

Finally, we deliver a simple nonparametric estimator of the asymptotic variance of the Hill estimator and prove consistency for processes with NED extremes.

Assume that observations are generated from nonstationary autoregressive (AR) processes of infinite order. We adopt a finite-order approximation model to predict future observations and obtain an asymptotic expression for the mean-squared prediction error (MSPE) of the least squares predictor. This expression provides the first exact assessment of the impacts of nonstationarity, model complexity, and model misspecification on the corresponding MSPE. It not only provides a deeper understanding of the least squares predictors in nonstationary time series, but also forms the theoretical foundation for a companion paper by the same authors, which obtains asymptotically efficient order selection in nonstationary AR processes of possibly infinite order.

We analyze the properties of the conventional Gaussian-based cointegrating rank tests of Johansen (1996, Likelihood-Based Inference in Cointegrated Vector Autoregressive Models) in the case where the vector of series under test is driven by globally stationary, conditionally heteroskedastic (martingale difference) innovations. We first demonstrate that the limiting null distributions of the rank statistics coincide with those derived by previous authors who assume either independent and identically distributed (i.i.d.) or (strict and covariance) stationary martingale difference innovations. We then propose wild bootstrap implementations of the cointegrating rank tests and demonstrate that the associated bootstrap rank statistics replicate the first-order asymptotic null distributions of the rank statistics. We show that the same is also true of the corresponding rank tests based on the i.i.d. bootstrap of Swensen (2006, Econometrica 74, 1699–1714). The wild bootstrap, however, has the important property that, unlike the i.i.d. bootstrap, it preserves in the resampled data the pattern of heteroskedasticity present in the original shocks. Consistent with this, numerical evidence suggests that, relative to tests based on the asymptotic critical values or the i.i.d. bootstrap, the wild bootstrap rank tests perform very well in small samples under a variety of conditionally heteroskedastic innovation processes. An empirical application to the term structure of interest rates is given.

We develop a nonparametric regression-based goodness-of-fit test for multifactor continuous-time Markov models using the conditional characteristic function, which often has a convenient closed form or can be approximated accurately for many popular continuous-time Markov models in economics and finance. An omnibus test fully utilizes the information in the joint conditional distribution of the underlying processes and hence has power against a vast class of continuous-time alternatives in the multifactor framework. A class of easy-to-interpret diagnostic procedures is also proposed to gauge possible sources of model misspecification. All the proposed test statistics have a convenient asymptotic N(0, 1) distribution under correct model specification, and all asymptotic results allow for some data-dependent bandwidth. Simulations show that in finite samples, our tests have reasonable size, thanks to the dimension reduction in nonparametric regression, and good power against a variety of alternatives, including misspecifications in the joint dynamics, but the dynamics of each individual component is correctly specified. This feature is not attainable by some existing tests. A parametric bootstrap improves the finite-sample performance of proposed tests but with a higher computational cost.

This paper derives some exact power properties of tests for spatial autocorrelation in the context of a linear regression model. In particular, we characterize the circumstances in which the power vanishes as the autocorrelation increases, thus extending the work of Krämer (2005). More generally, the analysis in the paper sheds new light on how the power of tests for spatial autocorrelation is affected by the matrix of regressors and by the spatial structure. We mainly focus on the problem of residual spatial autocorrelation, in which case it is appropriate to restrict attention to the class of invariant tests, but we also consider the case when the autocorrelation is due to the presence of a spatially lagged dependent variable among the regressors. A numerical study aimed at assessing the practical relevance of the theoretical results is included.

This paper considers inference based on a test statistic that has a limit distribution that is discontinuous in a parameter. The paper shows that subsampling and m out of n bootstrap tests based on such a test statistic often have asymptotic size—defined as the limit of exact size—that is greater than the nominal level of the tests. This is due to a lack of uniformity in the pointwise asymptotics. We determine precisely the asymptotic size of such tests under a general set of high-level conditions that are relatively easy to verify. The results show that the asymptotic size of subsampling and m out of n bootstrap tests is distorted in some examples but not in others.

Linearity in a causal relationship between a dependent variable and a set of regressors is a common assumption throughout economics. In this paper we consider the case when the coefficients in this relationship are random and distributed independently from the regressors. Our aim is to identify and estimate the distribution of the coefficients nonparametrically. We propose a kernel-based estimator for the joint probability density of the coefficients. Although this estimator shares certain features with standard nonparametric kernel density estimators, it also differs in some important characteristics that are due to the very different setup we are considering. Most importantly, the kernel is nonstandard and derives from the theory of Radon transforms. Consequently, we call our estimator the Radon transform estimator (RTE). We establish the large sample behavior of this estimator—in particular, rate optimality and asymptotic distribution. In addition, we extend the basic model to cover extensions, including endogenous regressors and additional controls. Finally, we analyze the properties of the estimator in finite samples by a simulation study, as well as an application to consumer demand using British household data.

This paper considers the problem of predicting binary choices by selecting from a possibly large set of candidate explanatory variables, which can include both exogenous variables and lagged dependent variables. We consider risk minimization with the risk function being the predictive classification error. We study the convergence rates of empirical risk minimization in both the frequentist and Bayesian approaches. The Bayesian treatment uses a Gibbs posterior constructed directly from the empirical risk instead of using the usual likelihood-based posterior. Therefore these approaches do not require a correctly specified probability model. We show that the proposed methods have near optimal performance relative to a class of linear classification rules with selected variables. Such results in classification are obtained in a framework of dependent data with strong mixing.

We consider two tests of structural change for partially linear time-series models. The first tests for structural change in the parametric component, based on the cumulative sums of gradients from a single semiparametric regression. The second tests for structural change in the parametric and nonparametric components simultaneously, based on the cumulative sums of weighted residuals from the same semiparametric regression. We derive the limiting distributions of both tests under the null hypothesis of no structural change and for sequences of local alternatives. We show that the tests are generally not asymptotically pivotal under the null but may be free of nuisance parameters asymptotically under further asymptotic stationarity conditions. Our tests thus complement the conventional instability tests for parametric models. To improve the finite-sample performance of our tests, we also propose a wild bootstrap version of our tests and justify its validity. Finally, we conduct a small set of Monte Carlo simulations to investigate the finite-sample properties of the tests.

This paper considers a formulation of the extended constant or time-varying conditional correlation GARCH model that allows for volatility feedback of either the positive or negative sign. In the previous literature, negative volatility spillovers were ruled out by the assumption that all the parameters of the model are nonnegative, which is a sufficient condition for ensuring the positive definiteness of the conditional covariance matrix. In order to allow for negative feedback, we show that the positive definiteness of the conditional covariance matrix can be guaranteed even if some of the parameters are negative. Thus, we extend the results of Nelson and Cao (1992) and Tsai and Chan (2008) to a multivariate setting. For the bivariate case of order one, we look into the consequences of adopting these less severe restrictions and find that the flexibility of the process is substantially increased. Our results are helpful for the model-builder, who can consider the unrestricted formulation as a tool for testing various economic theories.

In this paper, we extend the GMM framework for the estimation of the mixed-regressive spatial autoregressive model by Lee(2007a) to estimate a high order mixed-regressive spatial autoregressive model with spatial autoregressive disturbances. Identification of such a general model is considered. The GMM approach has computational advantage over the conventional ML method. The proposed GMM estimators are shown to be consistent and asymptotically normal. The best GMM estimator is derived, within the class of GMM estimators based on linear and quadratic moment conditions of the disturbances. The best GMM estimator is asymptotically as efficient as the ML estimator under normality, more efficient than the QML estimator otherwise, and is efficient relative to the G2SLS estimator.

This paper considers parametric estimation problems with independent, identically nonregularly distributed data. It focuses on rate efficiency, in the sense of maximal possible convergence rates of stochastically bounded estimators, as an optimality criterion, largely unexplored in parametric estimation. Under mild conditions, the Hellinger metric, defined on the space of parametric probability measures, is shown to be an essentially universally applicable tool to determine maximal possible convergence rates. These rates are shown to be attainable in general classes of parametric estimation problems.