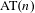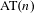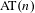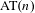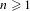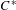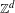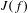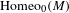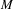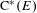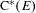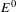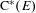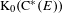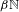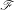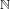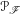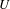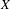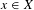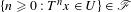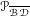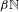Contents
Original Article
Entropy of
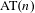 $\text{AT}(n)$ systems
$\text{AT}(n)$ systems
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1118-1126
-
- Article
- Export citation
Continuous orbit equivalence rigidity
-
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1543-1563
-
- Article
- Export citation
On dynamical systems preserving weights
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 2729-2747
-
- Article
- Export citation
Topologically completely positive entropy and zero-dimensional topologically completely positive entropy
-
- Published online by Cambridge University Press:
- 14 March 2017, pp. 1894-1922
-
- Article
- Export citation
The dynamical zeta function for commuting automorphisms of zero-dimensional groups
-
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1564-1587
-
- Article
- Export citation
The escaping set of transcendental self-maps of the punctured plane
-
- Published online by Cambridge University Press:
- 13 October 2016, pp. 739-760
-
- Article
- Export citation
Large-scale geometry of homeomorphism groups
-
- Published online by Cambridge University Press:
- 03 April 2017, pp. 2748-2779
-
- Article
- Export citation
Traces on topological-graph algebras
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1923-1953
-
- Article
- Export citation
Research Article
Linear dynamics and recurrence properties defined via essential idempotents of
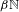 $\unicode[STIX]{x1D6FD}\mathbb{N}$
$\unicode[STIX]{x1D6FD}\mathbb{N}$
-
- Published online by Cambridge University Press:
- 13 July 2016, pp. 285-300
-
- Article
- Export citation
Original Article
Hyperbolicity versus weak periodic orbits inside homoclinic classes
-
- Published online by Cambridge University Press:
- 14 March 2017, pp. 2345-2400
-
- Article
- Export citation
Central limit theorems for sequential and random intermittent dynamical systems
-
- Published online by Cambridge University Press:
- 22 September 2016, pp. 1127-1153
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 38 Issue 8 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
On equilibrium states for partially hyperbolic horseshoes
-
- Published online by Cambridge University Press:
- 04 July 2016, pp. 301-335
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 38 Issue 8 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Original Article
Equilibrium measures for certain isometric extensions of Anosov systems
-
- Published online by Cambridge University Press:
- 22 September 2016, pp. 1154-1167
-
- Article
- Export citation
A note on subgroups of automorphism groups of full shifts
-
- Published online by Cambridge University Press:
- 08 November 2016, pp. 1588-1600
-
- Article
- Export citation
The error term in the prime orbit theorem for expanding semiflows
-
- Published online by Cambridge University Press:
- 24 January 2017, pp. 1954-2000
-
- Article
- Export citation
Invariant circles and depinning transition
-
- Published online by Cambridge University Press:
- 22 September 2016, pp. 761-787
-
- Article
- Export citation
Geometric results on linear actions of reductive Lie groups for applications to homogeneous dynamics
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 2780-2800
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 38 Issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 27 July 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation