The stress–elastic strain relationship is studied for a composite under a plastic deformation. The constitutive law of each component is described by a deformation theory of strain gradient plasticity which introduces an internal length scale. The conventional deformation plastic theory is obtained when the internal length scale tends to 0. The Hashin–Shtrikman upper bound for a two-phase composite governed by a power law is derived. It is predicted, by differentiating the bounds, that in most cases, the stress and the elastic strain follow a non-linear relation immediately after the elastic range. However, for some particular values of the ratio of the internal length scale and the micro-scale of the composite, this relation is linear. The prediction is illustrated by various numerical examples.

We consider the thermal insulation property of homogeneous anisotropically heat-conducting bodies, i.e. those whose thermal tensor (matrix) A is constant throughout the body but not generally a constant times the identity. This anisotropy is a common feature of nano-composite materials. We propose using the principal Dirichlet eigenvalue λ of the associated elliptic differential operator −∇ ⋅ A∇ as a simple measurement for the insulating ability of the material, because the time scale of thermal flow is of the order of 1/λ. 1/λ is a generalization of the ‘R-value’ used in engineering practice as a measure of the insulating ability of isotropic conductors. If the thermal tensor A depends on parameters, e.g. inherited from nanostructure, then so does λ. It is important to know how λ depends on the parameters. For the material to be a good insulator, λ should be suppressed. But calculation or estimation of this principal elliptic eigenvalue, particularly over ranges of parameter values, is not a simple task. The focus of this paper is estimation – by fitted formulas and new exact bounds – of the principal elliptic Dirichlet eigenvalue of ellipses (2D) and ellipsoids (3D) using only simple expressions in the eigenvalues of the matrix A. Our simplest approximations and bounds avoid even the calculation of matrix eigenvalues and use in 2D merely the trace and determinant of A, and in 3D the trace and determinant of A and the trace of A2. The new bounds are shown to imply an extremal property in homogenization theory and a new condition for enhancement in Taylor dispersion. Recently, Zheng, Forest, Lipton, Zhou and Wang published formulas for the thermal tensor A in the case of strong extensional fiber-type flow of a polymer with dilute rod-like nano-inclusions, including explicitly the influence of the probability distribution of inclusion orientation. Our results are combined with these formulas to quantify the effect of variations of the probability distribution on the insulating ability of the composite.

The static compression between two smooth plates of an axisymmetric capsule or vesicle is investigated by means of asymptotic analysis. The governing equations of the vesicle are derived from thin-shell theory and involve a bending stiffness B, a shear modulus H, the unstressed vesicle radius a and a constant surface-area constraint. The sixth-order free-boundary problem obtained by a balance-of-forces approach is addressed in the limit when the dimensionless parameter C = Ha2/B is large and the plate displacements are small. When the plate displacement is of order aC−1/2, the vesicle undergoes a sub-critical buckling instability which is captured by leading-order asymptotics. Asymptotic linear and quadratic force–displacement relations for the pre- and post-buckled solutions are determined. The leading-order post-buckled solution is described by a simple fourth-order problem, exhibiting stress-focusing with stretching and bending confined to a narrow boundary layer. In contrast, in the pre-buckled state, stretching occurs over a larger length scale than bending. The results are in good qualitative agreement with numerical simulations for finite values of C.

We consider a mathematical model which describes the frictional contact between a piezoelectric body and a foundation. The material behaviour is modelled with a non-linear electro-elastic constitutive law, the contact is bilateral, the process is static and the foundation is assumed to be electrically conductive. Both the friction law and the electrical conductivity condition on the contact surface are described with subdifferential boundary conditions. We derive a variational formulation of the problem which is of the form of a system of two coupled hemi-variational inequalities for the displacement and the electric potential fields, respectively. Then we prove the existence of a weak solution to the model and, under additional assumptions, its uniqueness. The proof is based on an abstract result on operator inclusions in Banach spaces.

In contrast to single-product pricing models, multi-product pricing models have been much less studied because of the complexity of multi-product demand functions. It is highly non-trivial to construct a multi-product demand function on the entire set of non-negative prices, not to mention approximating the real market demands to a desirable accuracy. Thus, many decision makers use incomplete demand functions which are defined only on a restricted domain, e.g. the set where all components of demand functions are non-negative. In the first part of this paper, we demonstrate the necessity of defining demand functions on the entire set of non-negative prices through some examples. Indeed, these examples show that incomplete demand functions may lead to inferior pricing models. Then we formulate a type of demand functions using a Nonlinear Complementarity Problem (NCP). We call it a Complementarity-Constrained Demand Function (CCDF). We will show that such demand functions possess certain desirable properties, such as monotonicity. In the second part of the paper, we consider an oligopolistic market, where producers/sellers are playing a non-cooperative game to determine the prices of their products. When a CCDF is incorporated into the best response problem of each producer/seller involved, it leads to a complementarity constrained pricing problem facing each producer/seller. Some basic properties of the pricing models are presented. In particular, we show that, under certain conditions, the complementarity constraints in this pricing model can be eliminated, which tremendously simplifies the computation and theoretical analysis.

We present a two-dimensional micro-scale model for crystal dissolution and precipitation in a porous medium. The local geometry of the pore is represented as a thin strip and the model allows for changes in the pore volume. A formal limiting argument, for the limit of the width of the strip going to zero, leads to a system of one-dimensional effective upscaled equations. We show that the effective equations allow for travelling-wave solutions and prove the existence and uniqueness of these. Numerical solutions of the effective equations are compared with numerical solutions of the original equations on the thin strip and with analytical results. We also show that a model from the literature that does not allow changes in the pore volume can be obtained from the present model as a formal limit.

This paper deals with a new method to determine the dependence of the electrical conductivity of metals or semiconductors on temperature. It is based on the fact that the current–voltage relationship is easily measurable. This inverse problem is solved by the classical Abel integral equation.

We present a stability result for a class of non-trivial self-similarly vanishing solutions to a 3D Hele-Shaw moving boundary problem with surface tension and single-point suction. These solutions are domains that bifurcate from the trivial spherical solution. The moving domains have a geometric centre located at the suction point and they are axially symmetric. We show stability with respect to perturbations that preserve these properties.

A configuration of near-equilibrium liquid droplets sitting on a precursor film which wets the entire substrate can coarsen in time by two different mechanisms: collapse or collision of droplets. The collapse mechanism, i.e., a larger droplet grows at the expense of a smaller one by mass exchange through the precursor film, is also known as Ostwald ripening. As was shown by K. B. Glasner and T. P. Witelski (‘Collision versus collapse of droplets in coarsening of dewetting thin films’, Phys. D209 (1–4), 2005, 80–104) in case of a one-dimensional substrate, the migration of droplets may interfere with Ostwald ripening: The configuration can coarsen by collision rather than by collapse. We study the role of migration in a two-dimensional substrate for a whole range of mobilities. We characterize the velocity of a single droplet immersed into an environment with constant flux field far away. This allows us to describe the dynamics of a droplet configuration on a two-dimensional substrate by a system of ODEs. In particular, we find by heuristic arguments that collision can be a relevant coarsening mechanism.

In this paper, we consider the asymptotic behaviour for the non-local parabolic problem 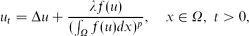with a homogeneous Dirichlet boundary condition, where λ > 0, p > 0 and f is non-increasing. It is found that (a) for 0 < p ≤ 1, u(x, t) is globally bounded and the unique stationary solution is globally asymptotically stable for any λ > 0; (b) for 1 < p < 2, u(x, t) is globally bounded for any λ > 0; (c) for p = 2, if 0 < λ < 2|∂Ω|2, then u(x, t) is globally bounded; if λ = 2|∂Ω|2, there is no stationary solution and u(x, t) is a global solution and u(x, t) → ∞ as t → ∞ for all x ∈ Ω; if λ > 2|∂Ω|2, there is no stationary solution and u(x, t) blows up in finite time for all x ∈ Ω; (d) for p > 2, there exists a λ* > 0 such that for λ > λ*, or for 0 < λ ≤ λ* and u0(x) sufficiently large, u(x, t) blows up in finite time. Moreover, some formal asymptotic estimates for the behaviour of u(x, t) as it blows up are obtained for p ≥ 2.

We study an electrical conduction problem in biological tissues in the radiofrequency range, which is governed by an elliptic equation with memory. We prove the time exponential asymptotic stability of the solution. We provide in this way both a theoretical justification to the complex elliptic problem currently used in electrical impedance tomography and additional information on the structure of the complex coefficients appearing in the elliptic equation. Our approach relies on the fact that the elliptic equation with memory is the homogenisation limit of a sequence of problems for which we prove suitable uniform estimates.

In this paper, we are interested in the mathematical and numerical study of the Prigozhin model for a growing sandpile. Based on implicit Euler discretization in time, we give a simple improvement of theoretical and numerical analyses of the dual formulation for the problem. By using this model, we also give some application to the Monge–Kantorovich problem for optimal mass transportation.

A two component system driven by both interface area and interface curvature is studied with a new phase field model. We show that if the curvature impact in the system is strong enough, there exist bubble profiles. A bubble profile describes a pattern of an inner core of one component surround by an outer membrane of the other component. It is a radial solution to a fourth-order nonlinear partial differential equation. We show the existence of such profiles in all dimensions, although the profile is unstable if the dimension is greater than 2.

The dynamics and oscillatory instabilities of multi-spike solutions to the one-dimensional Gray-Scott reaction–diffusion system on a finite domain are studied in a particular parameter regime. In this parameter regime, a formal singular perturbation method is used to derive a novel ODE–PDE Stefan problem, which determines the dynamics of a collection of spikes for a multi-spike pattern. This Stefan problem has moving Dirac source terms concentrated at the spike locations. For a certain subrange of the parameters, this Stefan problem is quasi-steady and an explicit set of differential-algebraic equations characterizing the spike dynamics is derived. By analysing a nonlocal eigenvalue problem, it is found that this multi-spike quasi-equilibrium solution can undergo a Hopf bifurcation leading to oscillations in the spike amplitudes on an O(1) time scale. In another subrange of the parameters, the spike motion is not quasi-steady and the full Stefan problem is solved numerically by using an appropriate discretization of the Dirac source terms. These numerical computations, together with a linearization of the Stefan problem, show that the spike layers can undergo a drift instability arising from a Hopf bifurcation. This instability leads to a time-dependent oscillatory behaviour in the spike locations.

Ventricular assist devices (VADs) provide long- and short-term support to chronically ill heart disease patients; these devices are expected to match the remarkable functionality of the natural heart, which makes their design a very challenging task. Blood pumps, the principal component of the VADs, must operate over a wide range of flow rates and pressure heads and minimise the damage to blood cells in the process. They should also be small to allow easy implantation in both children and adults. Mathematical methods and computational fluid dynamics (CFD) have recently emerged as powerful design tools in this context; a review of the recent advances in the field is presented here. This review focusses on the CFD-based design strategies applied to blood flow in blood pumps and other blood-handling devices. Both simulation methods for blood flow and blood damage models are reviewed. The literature is put into context with a discussion of the chronological development in the field. The review is illustrated with specific examples drawn from our group's Galerkin/least squares (GLS) finite-element simulations of the basic Newtonian flow problem for the continuous-flow centrifugal GYRO blood pump. The GLS formulation is outlined, and modifications to include models that better represent blood rheology are shown. Haemocompatibility analysis of the pump is reviewed in the context of haemolysis estimations based on different blood damage models. Our strain-based blood damage model that accounts for the viscoleasticity associated with the red blood cells is reviewed in detail. The viability of design improvement based on trial and error and complete simulation-based design optimisation schemes are also discussed.

Lie symmetry analysis is applied to study the non-linear rotating shallow-water equations. The 9-dimensional Lie algebra of point symmetries admitted by the model is found. It is shown that the rotating shallow-water equations can be transformed to the classical shallow-water model. The derived symmetries are used to generate new exact solutions of the rotating shallow-water equations. In particular, a new class of time-periodic solutions with quasi-closed particle trajectories is constructed and studied. The symmetry reduction method is also used to obtain some invariant solutions of the model. Examples of these solutions are presented with a brief physical interpretation.

Motivated by a recent investigation of Millar and McKay [Director orientation of a twisted nematic under the influence of an in-plane magnetic field. Mol. Cryst. Liq. Cryst435, 277/[937]–286/[946] (2005)], we study the magnetic field twist-Fréedericksz transition for a nematic liquid crystal of positive diamagnetic anisotropy with strong anchoring and pre-twist boundary conditions. Despite the pre-twist, the system still possesses ℤ2 symmetry and a symmetry-breaking pitchfork bifurcation, which occurs at a critical magnetic-field strength that, as we prove, is above the threshold for the classical twist-Fréedericksz transition (which has no pre-twist). It was observed numerically by Millar and McKay that this instability occurs precisely at the point at which the ground-state solution loses its monotonicity (with respect to the position coordinate across the cell gap). We explain this surprising observation using a rigorous phase-space analysis.

Adhesion of cells to one another and their environment is an important regulator of many biological processes but has proved difficult to incorporate into continuum mathematical models. This paper develops further the new modelling approach proposed by Armstrong et al. (A continuum approach to modelling cell–cell adhesion, J. Theor. Biol. 243: 98–113, 2006). The models studied in the present paper use an integro-partial differential equation for cell behaviour, in which the integral represents the sensing by cells of their local environment. This enables an effective representation of cell–cell adhesion, as well as random cell movement, and cell proliferation. The authors use this modelling approach to investigate the ability of cell–cell adhesion to generate spatial patterns during cell aggregation. The model is also extended to give a new representation of cancer growth, whose solutions reflect the balance between cell–cell and cell–matrix adhesion in regulating cancer invasion. The non-local term in these models means that there is no standard theory from which one can deduce the boundedness required for biological realism: specifically, solutions for cell density must lie between zero and a positive density corresponding to close cell packing. Here the authors derive a number of conditions, each of which is sufficient for the required boundedness, and they demonstrate numerically that cell density increases above the upper bound for some parameter sets not satisfying these conditions. Finally the authors outline what they regard as the main mathematical challenges for future work on boundedness in models of this type.

We study the stability and dynamics of melting icebergs. Specifically, we address the ‘toppling’ or ‘rollover’ observed for floating icebergs. The rollover is thought to occur because the ocean melts the iceberg from below, causing its overall mass and mass distribution to change with time. We model the evolution of equilibrium positions for a general homogeneous body afloat in an ideal fluid, as this homogeneous body is subjected to ‘melting’, i.e. a slow removal of material from the submerged part. If this process is the dominating melting mechanism, can the likelihood of a toppling be inferred from observing only the above-surface part? We show here that some information about the evolution of stability due to melting can be inferred from the surface geometry of the iceberg.

We consider a solution of a mono-component oil and wax. The latter is dissolved in the oil if the temperature is above the so-called cloud point (which depends on the concentration) and it segregates in the form of solid crystals if temperature is below the cloud point. As the solid fraction of wax increases, the diffusivity of liquid wax in the oil decreases (gelification), eventually vanishing. We study a one-dimensional model where temperature is initially above the cloud point and then it is lowered to induce diffusion and gelification. We formulate the relevant mathematical problem (a free boundary problem), studying its well-posedness and showing some qualitative results.