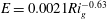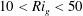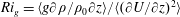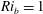Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 4
Transient behaviour of a rarefied gas around a sphere caused by impulsive rotation
-
- Published online by Cambridge University Press:
- 23 December 2020, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 4
Planar potential flow on Cartesian grids
-
- Published online by Cambridge University Press:
- 27 April 2022, A19
-
- Article
- Export citation
- Cited by 4
Theory of vaporization of a rigid spherical droplet in slowly varying rectilinear flow at low Reynolds numbers
-
- Published online by Cambridge University Press:
- 21 May 2007, pp. 219-249
-
- Article
- Export citation
- Cited by 4
Numerical study of viscous starting flow past wedges
-
- Published online by Cambridge University Press:
- 19 July 2016, pp. 150-165
-
- Article
- Export citation
- Cited by 4
Entropy budget and coherent structures associated with a spectral closure model of turbulence
-
- Published online by Cambridge University Press:
- 29 October 2018, pp. 806-822
-
- Article
- Export citation
- Cited by 4
Lagrangian stochastic modelling of acceleration in turbulent wall-bounded flows
-
- Published online by Cambridge University Press:
- 14 April 2020, A38
-
- Article
- Export citation
- Cited by 4
Stability analysis of natural convection in a cavity; walls with uniform heat or mass flux
-
- Published online by Cambridge University Press:
- 10 July 1999, pp. 45-73
-
- Article
- Export citation
- Cited by 4
Is the Taylor–Proudman theorem exact in unbounded domains? Case study of the three-dimensional stability of a vortex pair in a rapidly rotating fluid
-
- Published online by Cambridge University Press:
- 08 June 2021, R1
-
- Article
- Export citation
- Cited by 4
Entrainment across a sheared density interface in a cavity flow
-
- Published online by Cambridge University Press:
- 29 November 2017, pp. 999-1021
-
- Article
- Export citation
- Cited by 4
Onset of convection in two layers of a binary liquid
-
- Published online by Cambridge University Press:
- 18 March 2010, pp. 105-124
-
- Article
- Export citation
- Cited by 4
Linear and nonlinear responses to harmonic force in rotating flow
-
- Published online by Cambridge University Press:
- 04 May 2016, pp. 306-317
-
- Article
- Export citation
- Cited by 4
Unsteady convective–diffusive transport in semicircular microchannels with irreversible wall reaction
-
- Published online by Cambridge University Press:
- 21 September 2022, A1
-
- Article
- Export citation
- Cited by 4
Interface coupling effect and multi-mode Faraday instabilities in a three-layer fluid system
-
- Published online by Cambridge University Press:
- 01 March 2024, A8
-
- Article
- Export citation
- Cited by 4
Numerical studies on the dynamics of an open triangle in a vertically oscillatory flow
-
- Published online by Cambridge University Press:
- 05 January 2016, pp. 381-406
-
- Article
- Export citation
- Cited by 4
Approximate theory of acoustic waveguide of metamaterials
-
- Published online by Cambridge University Press:
- 12 April 2011, pp. 203-220
-
- Article
- Export citation
- Cited by 4
Closing the loop: nonlinear Taylor vortex flow through the lens of resolvent analysis
-
- Published online by Cambridge University Press:
- 04 August 2021, A9
-
- Article
- Export citation
- Cited by 4
Lagrangian blocking in highly viscous shear flows past a sphere
-
- Published online by Cambridge University Press:
- 16 February 2011, pp. 120-166
-
- Article
- Export citation
- Cited by 4
Long-lived and unstable modes of Brownian suspensions in microchannels
-
- Published online by Cambridge University Press:
- 10 May 2012, pp. 407-418
-
- Article
- Export citation
- Cited by 4
Uncertainty propagation in model extraction by system identification and its implication for control design
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 214-236
-
- Article
- Export citation
- Cited by 4
Turbulence distortion and blockage in the induction zone of a horizontal axis turbine
-
- Published online by Cambridge University Press:
- 25 November 2024, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation