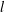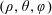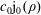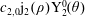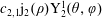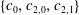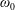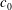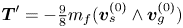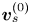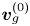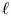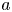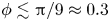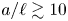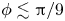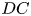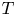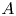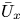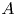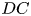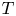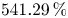Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 3
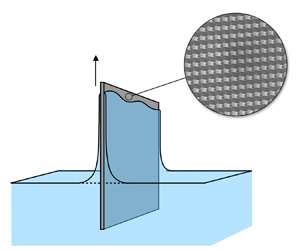
Surface corrugations induce helical near-surface flows and transport in microfluidic channels
-
- Published online by Cambridge University Press:
- 11 March 2024, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Turbulent flow around convex curved tandem cylinders
-
- Published online by Cambridge University Press:
- 17 October 2024, A58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
A stable precessing quasi-geostrophic vortex model with distributed potential vorticity
-
- Published online by Cambridge University Press:
- 02 March 2020, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Inertial torque on a squirmer
-
- Published online by Cambridge University Press:
- 07 December 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Hydrodynamic permeability of circular-inclusion-doped Brinkman media
-
- Published online by Cambridge University Press:
- 02 October 2023, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Heat and momentum transfer to a particle in a laminar boundary layer
-
- Published online by Cambridge University Press:
- 24 February 2020, A6
-
- Article
- Export citation
- Cited by 3
Coating thickness prediction for a viscous film on a rough plate
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2024, A59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Temporal modulation on mixed convection in turbulent channels
-
- Published online by Cambridge University Press:
- 06 March 2025, A11
-
- Article
- Export citation
- Cited by 3
Analytic growth rate of gravitational instability in self-gravitating planar polytropes
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 362-399
-
- Article
- Export citation
- Cited by 3
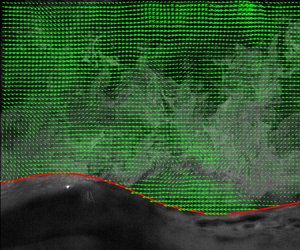
Turbulence over young wind waves dominated by capillaries and micro-breakers
-
- Published online by Cambridge University Press:
- 19 April 2024, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Connections between propulsive efficiency and wake structure via modal decomposition
-
- Published online by Cambridge University Press:
- 04 June 2024, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Pressure effects on mixing and combustion mode of a hydrogen/helium jet in cross-flow
-
- Published online by Cambridge University Press:
- 12 August 2025, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Fluid viscoelasticity affects ultrasound force field-induced particle transport
-
- Published online by Cambridge University Press:
- 28 November 2024, A75
-
- Article
- Export citation
- Cited by 3
Intermittent swimmers optimize energy expenditure with flick-to-flick motor control
-
- Published online by Cambridge University Press:
- 10 March 2025, A27
-
- Article
- Export citation
- Cited by 3
Obstacle arrangement can control flows through porous obstructions
-
- Published online by Cambridge University Press:
- 28 August 2024, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Significant influence of fluid viscoelasticity on flow dynamics past an oscillating cylinder
-
- Published online by Cambridge University Press:
- 16 November 2023, A26
-
- Article
- Export citation
- Cited by 3
Generalized Reynolds equation for microscale lubrication between eccentric circular cylinders based on kinetic theory
-
- Published online by Cambridge University Press:
- 27 October 2023, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Hydrodynamics and scaling laws for intermittent S-start swimming
-
- Published online by Cambridge University Press:
- 26 March 2024, A2
-
- Article
- Export citation
- Cited by 3
Relaminarization effects in hypersonic flow on a three-dimensional expansion–compression geometry
-
- Published online by Cambridge University Press:
- 22 April 2024, A25
-
- Article
- Export citation
- Cited by 3
Flow-induced oscillations of a transversely buckled flexible filament
-
- Published online by Cambridge University Press:
- 11 March 2025, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation