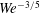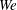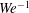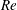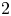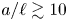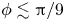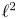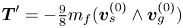Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 3
Hydrodynamics and scaling laws for intermittent S-start swimming
-
- Published online by Cambridge University Press:
- 26 March 2024, A2
-
- Article
- Export citation
- Cited by 3
Smoothed particle hydrodynamics modelling of particle-size segregation in granular flows
-
- Published online by Cambridge University Press:
- 24 January 2024, A47
-
- Article
- Export citation
- Cited by 3
Parameter dependences of the onset of turbulent liquid-jet breakup
-
- Published online by Cambridge University Press:
- 13 December 2016, R5
-
- Article
- Export citation
- Cited by 3
Membrane flutter induced by radiation of surface gravity waves on a uniform flow
-
- Published online by Cambridge University Press:
- 19 August 2020, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Modelling moving contact lines on inextensible elastic sheets in two dimensions
-
- Published online by Cambridge University Press:
- 16 January 2023, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Hydrodynamic permeability of circular-inclusion-doped Brinkman media
-
- Published online by Cambridge University Press:
- 02 October 2023, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Criteria for dynamic stall onset and vortex shedding in low-Reynolds-number flows
-
- Published online by Cambridge University Press:
- 26 September 2024, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Obstacle arrangement can control flows through porous obstructions
-
- Published online by Cambridge University Press:
- 28 August 2024, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Heat and momentum transfer to a particle in a laminar boundary layer
-
- Published online by Cambridge University Press:
- 24 February 2020, A6
-
- Article
- Export citation
- Cited by 3
Inertial torque on a squirmer
-
- Published online by Cambridge University Press:
- 07 December 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Effective viscosity of a dilute homogeneous suspension of spheres in Poiseuille flow between parallel slip walls
-
- Published online by Cambridge University Press:
- 20 July 2020, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 3
Two-fluid Euler theory of sound dispersion in gas mixtures of disparate masses
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 369-382
-
- Article
- Export citation
- Cited by 3
Instability of pressure-driven gas–liquid two-layer channel flows in two and three dimensions
-
- Published online by Cambridge University Press:
- 15 June 2018, pp. 1-34
-
- Article
- Export citation
- Cited by 3
Direct numerical simulation of turbulence–mean field interactions in a stably stratified fluid
-
- Published online by Cambridge University Press:
- 15 April 2002, pp. 213-242
-
- Article
- Export citation
- Cited by 3
Transverse instability of gravity–capillary solitary waves on deep water in the presence of constant vorticity
-
- Published online by Cambridge University Press:
- 03 June 2019, pp. 1028-1043
-
- Article
- Export citation
- Cited by 3
Geodynamics. By D. L. TURCOTTE & G. SCHUBERT. Cambridge University Press, 2002. 456 pp. ISBN 0-521-66624-4. £29.95.
-
- Published online by Cambridge University Press:
- 27 March 2003, pp. 410-411
-
- Article
- Export citation
- Cited by 3
Optimising the flow through a concertinaed filtration membrane
-
- Published online by Cambridge University Press:
- 26 February 2021, A28
-
- Article
- Export citation
- Cited by 3
Is spontaneous generation of coherent baroclinic flows possible?
-
- Published online by Cambridge University Press:
- 15 January 2019, pp. 889-923
-
- Article
- Export citation
- Cited by 3
Compressible exact solutions for one-dimensional laser ablation fronts
-
- Published online by Cambridge University Press:
- 09 August 2006, pp. 465-475
-
- Article
- Export citation
- Cited by 3
The motion of a layer of yield-stress material on an oscillating plate
-
- Published online by Cambridge University Press:
- 22 March 2023, A32
-
- Article
- Export citation