Refine listing
Actions for selected content:
Contents
Research Article
On lambda operations on mixed motives
-
- Published online by Cambridge University Press:
- 23 May 2013, pp. 381-404
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
KAG volume 12 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Tame kernels and second regulators of number fields and their subfields
-
- Published online by Cambridge University Press:
- 17 July 2013, pp. 137-165
-
- Article
- Export citation
Back Cover (IBC, OBC) and matter
KAG volume 12 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 27 January 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
On λ-invariants of number fields and étale cohomology
-
- Published online by Cambridge University Press:
- 05 July 2013, pp. 167-181
-
- Article
- Export citation
Back Cover (IBC, OBC) and matter
KAG volume 12 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 December 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
On a local to global principle in étale K-groups of curves
-
- Published online by Cambridge University Press:
- 17 May 2013, pp. 183-201
-
- Article
- Export citation
Hermitian periodicity and cohomology of infinite orthogonal groups
-
- Published online by Cambridge University Press:
- 23 May 2013, pp. 203-211
-
- Article
- Export citation
Front matter
KAG volume 12 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 October 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
KAG volume 12 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 30 October 2013, pp. b1-b2
-
- Article
-
- You have access
- Export citation
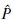 ) ∈
) ∈ 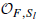 then
then