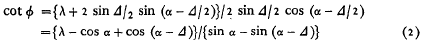Looking at the practical training for operators of future ships we are confronted with a wide range of sub-systems which may at some future date be grouped in a central ‘operations control’ point. The array shown in Fig. I is by no means exhaustive. The selection, education and training of personnel for the conduct of international shipping is of world importance and the United Kingdom has a wealth of experience which is respected by other maritime and would-be maritime nations. In this paper it is only possible to take a narrow and rather short-term view of requirements within the present manning and training structure.

The object of this paper is to describe how anticollision simulation is employed at H.M.S. Dryad, the Royal Navy School of Navigation. The methods described are those used in the Navy but this paper has no specific military slant, nor do the anti-collision problems studied at Dryad spring exclusively from the naval environment. Ship safety is one of the fundamentals of seamanship where the naval and mercantile problem is the same; the Navy does not however suffer the same manpower limitations on board ship.

The civil aviation problems in training navigators may appear simple compared with those of our marine colleagues, and possibly also in comparison to the military side of aviation. In civil aviation we are concerned with tactical problems but not to the same extent as in marine and military aviation, but there are those amongst us who can recall the halycon days of flying boats when we too were concerned with the tides and the state of the water. Since the end of the war there have been far reaching changes in civil aviation and navigation. The object used to be one of getting from A to B and battling a great deal with the unknown—long night hauls across the North Atlantic, Shannon and Keflavik, icy cold arrivals at Goose and Gander, pressure pattern flying and so on, with the minimum of navigation equipment, poor weather forecasting and limited range aircraft. Nowadays civil aircraft range is not the problem it used to be, although some such problems still exist, navigation equipment is more sophisticated and the A.T.C. requirements much more stringent. It is not so much getting from A to B as staying as close as possible to an assigned A.T.C. track.

The heart of the B.O.A.C. Navigation Procedures Trainer (NPT) is a general purpose digital computer (Elliotts 905) and the programs have been contained within a memory store of only 16,000 words. There are fourteen cubicles for the pupil navigators and one for the instructor. At each cubicle is the usual chart table and stowage for manuals; navigation information appears on a CRT screen in the form of letters and numbers. Requests for radio bearings, astro sights and so on are conveyed to the computer by means of a typewriter keyboard and some simple codes which are shown on a plaque to the left of the CRT. Only a few of the keys are special ones.

No. 6 Flying Training School at R.A.F. Finningley trains all R.A.F. ab initio navigators as well as refreshing the failing memories of its ageing qualified navigators, tasks which have been helped over the last 18 months by the introduction of an air navigation simulator based on a digital computer. The simulator can seat 15 students in three banks of 5, each bank being controlled by an instructor seated at a control console. The diagram on p. 267 shows the layout of one self-contained bank of 5 cubicles. In front of each console is a track display unit (TDU) on which the briefed route is traced drawn in ink on a ground glass screen. The students’ cubicles are instrumented to simulate the Dominie advanced navigation trainer but there are additional facilities so that Varsity sorties may be flown by students in their basic phase of training.

There have recently been various investigations of avoiding action when a ship is navigating by radar. The present paper attempts a numerical analysis of the changes in the apparent motion of the echo of the other vessel on the radarscope when both vessels alter course and speed simultaneously.

First we consider the case where the echo of the other vessel is approaching the centre of the radarscope—that is the vessels are on a collision course.

In Fig. I AOB represents a velocity triangle:

OA = own vessel's course and speed

OB = other vessel's course and speed

AB = other vessel's relative course and speed

When both vessels alter course, by Δα1 and Δα2 respectively, the velocity triangle becomes A′OB′ and A′B′ represents the new relative motion of the other vessel. If the triangle A′OB′ is rotated through Δα2 about O, and OB′ coincides with OB, the triangle is represented by BOC and < CDA′ = Δα2. The change θ in the other vessel's relative course caused by both vessels altering course by Δα1 and Δα2 respectively is therefore:

Now φ can be shown to satisfy the equation:

In conditions of poor visibility it is common practice to plot radar measurements of the range and relative bearing of other ships with respect to own ship and to deduce the relative tracks and passing distances. Radar equipment is available which can to a greater or lesser degree relieve the navigator of the tedium of plotting, and which could be developed into aids of considerable sophistication within the limits set by their cost. However, errors in measurement limit the precision with which relative tracks and passing distances can be computed. An alternative to radar plotting would be a data link between ships to broadcast measurements of course and speed on demand; a radar transponder would transmit the required information in coded form.

This suggestion is highly controversial, but it seems worthwhile to derive the mathematical relationship between errors in the data and the ensuing error in the calculated passing distance and to compare the errors using radar data and transponder data. The value of the comparison is however limited because likely errors in the data are not accurately known. The analysis of the radar plotting method is probably of interest in itself because the deficiencies of the method are derived with some rigour.

This paper was presented at a meeting of the Institute held in London on 12 January 1973 with the President, G. E. Beck, in the Chair. Mr. Prior, Director and General Manager of Kelvin Hughes, discusses factors influencing the commercial development of an innovation in navigational equipment and the inevitable time lag in production for the market. A technical description of Situation Display, the new marine radar system from Kelvin Hughes, was published in the April issue of this Journal. The discussion printed here relates both to Mr. Prior's paper and the technical description.

In this paper, based on an article printed on the back of the March 1973 issue of the Pilot Chart of the North Atlantic Ocean, Mr Fricker analyses three collisions that emphasize the necessity for adhering to the concepts of prudence and safety underlying the Rules of the Road; they are no less essential when navigating by radar in reduced visibility. Terms such as ‘right rudder’, readily understood, have not been altered to conform to English Martime parlance.

This paper is a sequel to the author's paper under the same title published in the April issue of the Journal.

Recent work on marine traffic engineering in Japan was reviewed in four papers published in this Journal in 1971. In the present paper, which may be regarded as a sequel to these, Professor Makishima offers some theoretical comments.

This paper discusses the drawbacks of observational methods of analysing navigational errors and shows the advantages of a synthesizing technique, whereby the effect of any change in the magnitude and distribution of a component error upon the overall resultant error can be evaluated and examined. To this end a computer program has been developed which is capable of accepting both analytical and numerical statistical distributions, representing errors in the components, and combining them to yield the overall effective error. A new error distribution better representative of many navigational error distributions is introduced. The work described is applicable to the investigation of any error which depends upon the interaction of many component errors and is not restricted to the navigation field. An extension of the method to mixed samples is indicated.

The paper describes the final step in the development of a universal computer program aimed at synthesizing navigational errors in order that they can be used in evaluating their effect on any proposed A.T.C. system. The investigation was commenced at the College of Aeronautics in 1963 and has been the subject of several published papers during the interim period.

The heart of an inertial navigation system is the Inertial Measuring Unit (I.M.U.) as this carries out the fundamental tasks of measuring the vehicle acceleration and providing a spatial reference. The I.M.U. thus determines the system performance and accuracy; it also accounts for about two thirds of the initial cost of the system and is a major factor in the cost of ownership.

Up to now the majority of IN systems have used a stable platform I.M.U. where the gyros and accelerometers are mounted on a gimbal suspended platform which is servo controlled from the gyros. This has greatly eased the task of developing suitable gyros of the required accuracy, as the gimbal stabilization system isolates the gyros from the angular motion of the vehicle and greatly simplifies the subsequent computation in terms of axis transformations; it provides a direct read out of the euler angles—heading, pitch and roll. However such a system is inevitably mechanically complex and its ultimate reliability is constrained by such components as slip rings, servo motors, synchros, resolvers, encoders, gimbal bearings &c.

The velocity of sound in water is a function of temperature, salinity and pressure. When an echo-sounder is used to make depth measurements, the time taken for a pulse to reach the ocean bed and return is measured. The machine is set to a standard sounding velocity, usually 800 or 820 fm/second (1463/1500 m/sec), and a nominal depth is recorded. This depth should then be corrected for the properties of the water. The ‘Tables of Velocity of Sound in Pure Water and Sea Water” by Matthews are commonly used for this purpose. Matthews compiled his tables using soundings taken by a number of research ships all over the world. He divided the oceans into 52 areas, and for each area calculated a set of depth corrections from 200 m to the ocean bottom. Since the tables were published more accurate measurements of velocity as a function of temperature, salinity and pressure have been made. There are also many more observations than were available when the tables were compiled. However, as these tables are in general use, no attempt has been made in this paper to change the corrections, and any computer results are therefore no more accurate than the tables.

When correcting depths manually aboard ship, the following procedure is followed. The depth on the echo-sounder is noted and entered into a log book. The position of the ship is known using some standard method of navigation such as satellite, Decca, Loran or radar.

A careful study of Parts A and B of the new Regulations as far as the application of the Steering and Sailing Rules is concerned leaves one disappointed and apprehensive. The first because an opportunity for considerable rationalization has not been fully used and the second because the corner-stone of the edifice of safety which for many years has supported the careful seaman has been knocked out. Apart from these there is a number of ambiguities.

It will be realized at once, of course, that these words are being written by one of the old school who has for several years opposed the more fundamental changes and to whom, since he first went to sea some sixty years ago, the old Rules covered with a minimum of verbiage the infinite variety of maritime circumstances and conditions. Additionally, having studied most of the collisions which have brought shipowners to Court, he has found none in which the Rules were faulted, but a vast majority in which human frailty in the form of misappraisal of the circumstances or conscious disobedience of one or more of the simple Rules had been the cause of disaster.

The corner-stone referred to above was the clear division of responsibility between the two parties to a situation involving collision risk in both the crossing and overtaking encounters.

Dr. David Lewis, a Fellow of this Institute and occasional contributor to the Journal, arrived at Palmer Station in the Antarctic, under jury rig, on 29 January having left Sydney on 20 October 1972 and stopped twenty-four hours at Stewart Island, N.Z., on the way. His long-term objective is to circumnavigate the Antarctic Continent, single-handed. He was twice capsized, in the course of which his gloves disappeared which resulted in badly frost-bitten fingers. After two months day and night in insulated boots, the warmth in the U.S. base when he arrived made his feet balloon and crack.

At the invitation of the Nautical Society of Japan, a society with aims similar to the Institute's, the Executive Secretary visited Japan between 5 and 17 April. A short report to Council follows.

Stewart very rightly draws attention to the practical value of the knot as a measure of velocity. In so doing he underlines one of the defects of SI: the essential simplicity and uniformity so attractive when considered in abstract becomes rather blurred when put into practice. The knot falls completely foul of SI; neither the unit of length nor that of time is an SI unit. The practical application of both units illustrate the difficulties well.

The choice of a standard set of prefixes to units, each separated by a factor of 1000, is both logical and convenient. One need never write down a number less than unity or greater than 999·999. … If the number is 1000 or more, it is divided by 1000 until it does lie within these limits and the appropriate prefix added to the unit. If it is less than unity, multiplication is substituted for division. For length measurements one starts with the metre and goes up to the kilometre, or down to the millimetre, micrometre and so on. Perhaps the only person whom this does not suit is the astronomer who is likely to prefer the light-year (approximately 10 metres, the index 16 being outside the range of prefixes) or the parsec (2·46 light-years).

The world, however, is not a linear one and difficulties start when one measures areas.

A recent Portuguese postage stamp of interest to philatelists and navigators alike was issued to commemorate the fiftieth anniversary of an adventurous air flight over the Atlantic from Portugal to Brazil by two officers of the Portuguese Navy, Rear-Admiral Cago Coutinho and Commander Sacadura Cabral.

In a valuable memoir published in English as well as in Portuguese by the Club Militar Naval of Lisbon an account of the novel method of navigation adopted by the two aviators is given. In the foreword to the memoir we are told:

‘The use of points of reference through the line of the intended crossing, and the able and skilful modifications of the formulae of nautical astronomy, by which the observer may, before starting, prepare the greater part of his calculations, in this way leaving only another quite material [small] part to be done in the air, are the two original conceptions by which the astronomical navigation, with a sextant, can be done in the air with accuracy and comfort …’