Let C be the closure of a recursively enumerable set B under some relation R. Suppose there is a primitive recursive relation Q, such that Q is a symmetric subrelation of R (i.e. if Q(m, n), then Q(n, m) and R(m, n)), and such that, for each m ϵ B, Q(m, n) for infinitely many n. Then there exists a primitive recursive set A, such that C is the closure under R of A. For proof, note that 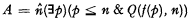 , where f is a primitive recursive function which enumerates B, has the required properties. For each m ϵ B, there is an n ϵ A, such that Q(m, n) and hence Q(n, m); therefore the closure of A under Q, and hence that under R, includes B. Conversely, since Q is a subrelation of R, A is included in C. Finally, that A is primitive recursive follows from [2] p. 180.
, where f is a primitive recursive function which enumerates B, has the required properties. For each m ϵ B, there is an n ϵ A, such that Q(m, n) and hence Q(n, m); therefore the closure of A under Q, and hence that under R, includes B. Conversely, since Q is a subrelation of R, A is included in C. Finally, that A is primitive recursive follows from [2] p. 180.
This observation can be applied to many formal systems S, by letting R correspond to the relation of deducibility in S, so that R(m, n) if and only if m is the Gödel number of a formula of S, or of a sequence of formulas, from which, together with axioms of S, a formula with the Gödel number n can be obtained by applications of rules of inference of S.