A set S of natural numbers is called recursively enumerable if there is a general recursive function F(x, y) such that
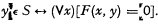
In other words, S is the projection of a two-dimensional general recursive set. Actually, it is no restriction on S to assume that F(x, y) is primitive recursive. If S is not empty, it is the range of the primitive recursive function
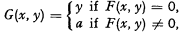
where a is a fixed element of S. Using pairing functions, we see that any non-empty recursively enumerable set is also the range of a primitive recursive function of one variable.
We use throughout the logical symbols ⋀ (and), ⋁ (or), → (if…then…), ↔ (if and only if), ∧ (for every), and ∨(there exists); negation does not occur explicitly. The variables range over the natural numbers, except as otherwise noted.
Martin Davis has shown that every recursively enumerable set S of natural numbers can be represented in the form
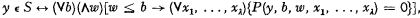
where P(y, b, w, x1 …, xλ) is a polynomial with integer coefficients. (Notice that this would not be correct if we replaced ≤ by <, since the right side of the equivalence would always be satisfied by b = 0.) Conversely, every set S represented by a formula of the above form is recursively enumerable. A basic unsolved problem is whether S can be defined using only existential quantifiers.