In this paper we discuss cylindric algebras with terms. The setting is two—sorted algebras—one sort for terms and one for Boolean elements. As with cylindric algebras, a cylindric algebra with terms has its roots in first order predicate logic [HMT1].
Let Σ be a set of sentences in a first order language with terms, equality and variables u0,u1,u2, …, Define a relation ≡Σ on Fm, the set of formulas, by φ ≡Σθ if and only if Σ ⊢ φ ↔ θ, and on Tm, the set of terms, by τ ≡Σσ if and only if Σ ⊢ τ ≈ σ. The operations +, ·, cκ, 0, 1 are defined as usual on equivalence classes. Define 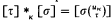 , where
, where 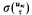 is σ with τ substituted for all occurrences of uκ. That the operation *κ, for κ < α, is well defined follows from the first order axioms of equality. Let vκ = [uκ]. To establish the link between terms and Booleans, define operations oκ as follows:
is σ with τ substituted for all occurrences of uκ. That the operation *κ, for κ < α, is well defined follows from the first order axioms of equality. Let vκ = [uκ]. To establish the link between terms and Booleans, define operations oκ as follows: 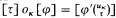 , where φ' is a variant of φ such that uκ is free for τ in φ′ and
, where φ' is a variant of φ such that uκ is free for τ in φ′ and 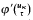 is φ′ with τ substituted for all free occurrences of uκ in φ′. From the first order axioms it follows that oκ, for κ < α, is well defined. Finally, instead of diagonal elements, we define a Boolean-valued operation on terms as follows: [τ] e [σ] = [τ ≈ σ].
is φ′ with τ substituted for all free occurrences of uκ in φ′. From the first order axioms it follows that oκ, for κ < α, is well defined. Finally, instead of diagonal elements, we define a Boolean-valued operation on terms as follows: [τ] e [σ] = [τ ≈ σ].