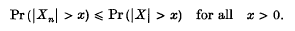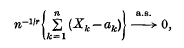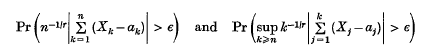Contents
Research Article
On integrals involving classical polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-420
-
- Article
- Export citation
Certain transformations of bilateral cognate trigonometrical series of the hypergeometric type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-424
-
- Article
- Export citation
Double Meijer transformations of certain hypergeometric functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-430
-
- Article
- Export citation
Some formulae for generalized Rice polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 431-434
-
- Article
- Export citation
A theorem on Kampé de Fériet function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 435-437
-
- Article
- Export citation
On a singular eigenvalue problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 439-446
-
- Article
- Export citation
On an integral equation arising in the theory of neutron streaming
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-453
-
- Article
- Export citation
An improved lower bound for the multidimensional dimer problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 455-463
-
- Article
- Export citation
Finite approximations to infinite non-negative matrices, II: refinements and applications
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 465-470
-
- Article
- Export citation
A note on the construction of confidence intervals for the coefficients of a second canonical variable
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 471-475
-
- Article
- Export citation
A note on the queueing system GI/G/∞
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 477-479
-
- Article
- Export citation
On the linear exponential family
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 481-483
-
- Article
- Export citation
Convergence rates in the law of large numbers. II†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-488
-
- Article
- Export citation
The generalization of Lagrange's expansion and the enumeration of trees: a correction
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 489
-
- Article
- Export citation
An infinite cylinder with multipole moments in general relativity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 491-501
-
- Article
- Export citation
Two dimensional mixed boundary-value problems in a wedge-shaped region
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 503-505
-
- Article
- Export citation
A note on a source in a rotating liquid
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 507-511
-
- Article
- Export citation
The flow of a micropolar liquid layer down an inclined plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 513-526
-
- Article
- Export citation
Free surface instability in electrohydrodynamics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 527-534
-
- Article
- Export citation
Contributions à l'étude des effets des extrémités dans un générateur à électrodes finies
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 535-548
-
- Article
- Export citation
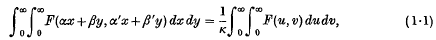
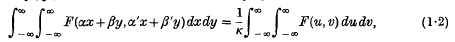

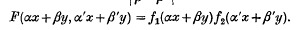
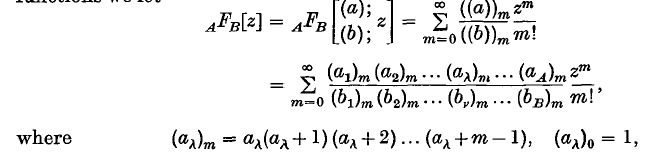
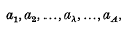
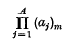
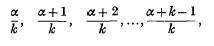
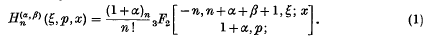
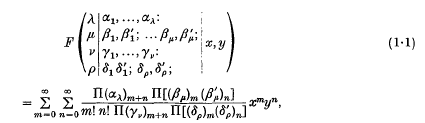
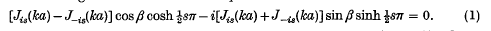
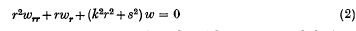
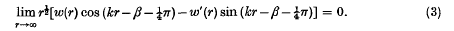


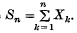 Suppose that the random vairables
Suppose that the random vairables