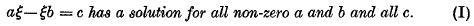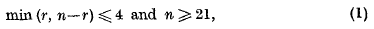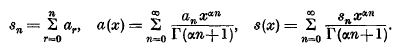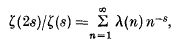Contents
Research Article
An application in hydrodynamics of the Green's function of an elastic plate
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 85-92
-
- Article
- Export citation
Some extremal problems for convex bodies
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-102
-
- Article
- Export citation
On a class of simple rings
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-117
-
- Article
- Export citation
Note on a sphere theorem for the axisymmetric stokes flow of a viscous fluid
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 118-121
-
- Article
- Export citation
Indefinite quadratic forms
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-124
-
- Article
- Export citation
Note on a plane measure problem
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-127
-
- Article
- Export citation
On Borel-type methods of summability
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-133
-
- Article
- Export citation
A doublet technique for solving Oseen's equations of axisymmetric flow
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 134-140
-
- Article
- Export citation
A disproof of a conjecture of Pólya
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-145
-
- Article
- Export citation
Entity-structure
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 146-160
-
- Article
- Export citation
Index
Index to volume 5
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 161
-
- Article
- Export citation
Front matter
MTK volume 5 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
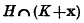 is not empty, of the volume
is not empty, of the volume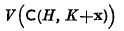
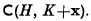 . The object of this paper is to discuss some of the more interesting consequences of the following general theorem.
. The object of this paper is to discuss some of the more interesting consequences of the following general theorem.