Contents
Research Article
Some metrical properties of continued fractions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-132
-
- Article
- Export citation
On Kruskal's cascades and counting containments in a set of subsets
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-141
-
- Article
- Export citation
An analytic inequality
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-152
-
- Article
- Export citation
Front matter
MTK volume 30 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
MTK volume 30 issue 1 Back matter
-
- Published online by Cambridge University Press:
- 26 February 2010, p. b1
-
- Article
-
- You have access
- Export citation
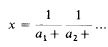
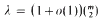 ,
,