Contents
Research Article
On the lower bound sieve
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-286
-
- Article
- Export citation
Large irregularities in sets of multiples and sieves
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-135
-
- Article
- Export citation
A zero-free region for the Hecke L-functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 287-304
-
- Article
- Export citation
Some new Opial-type inequalities
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 136-142
-
- Article
- Export citation
Book Reviews
Book Reviews - N. I. Akhiezer. The Calculus of Variations. Harwood Academic Publishers. 1988, 280 pp., $134.00. - J. M. Ball, Editor. Material Instabilities in Continuum Mechanics and Related Mathematical Problems. Clarendon Press. 1988, 542 pp., £45 - M. Barnsley. Fractals Everywhere. Academic Press. 1988, 394 pp., $39.95. - R. D. Carmichael and D. Mitrovic. Distributions and Analytic Functions. Longman. 1989, 347 pp., £23·50. - P. Clement, S. Invernizzi, E. Mitidieri and I. I. Vrabie, Editors. Semigroup Theory and Applications. Marcel Dekker. 1989, 454 pp., $138 - J. M. Cordier and T. Porter. Shape Theory: Categorical Methods of Approximation. Ellis-Horwood. 1989, 207 pp., £29·95. - J. C. Diaz, Editor. Mathematics for Large-scale Computing. Marcel Dekker. 1989, 345 pp., $102. - J. Dieudonné. Treatise on Analysis, Vol. 10-VII. Academic Press. 1988, 366 pp., $69.95. - D. N. Dikranjan, I. R. Prodanov and L. N. Stoyanov. Topological Groups. Marcel Dekker. 1990, 287 pp., $119.50. - J. Fauvel, R. Flood, M. Shortland and R. Wilson, Editors. Let Newton be! A new perspective on his life and works. Oxford University Press. 1989, 272 pp., £8·95. - B. Fine. Algebraic Theory of the Bianchi Groups. Marcel Dekker. 1989, 249 pp., $119.50. - A. T. Fomenko. Symplectic Geometry. Gordon and Breach. 1988, 387 pp., $180. - M. D. Gunzburger. Finite Element Methods for Viscous Incompressible Flows—A Guide to Theory, Practice and Algorithms. Academic Press. 1989, 269 pp., $44.50. - J. Hilgert, K. H. Hofmann and J. D. Lawson. Lie Groups, Convex Cones and Semigroups. Clarendon Press. 1989, 645 pp., £55. - G. Hiss and K. Lux. Brauer Trees of Sporadic Groups. Clarendon Press. 1989, 526 pp., £40. - S. Hollingdale. Makers of Mathematics. Penguin Books. 1989, 433 pp., £7·99. - J. F. Humphreys and M. Y. Prest. Numbers, Groups and Codes. Cambridge University Press. 1989, 288 pp., £10·95. - C. U. Jensen and H. Lenzing. Model Theoretic Algebra. Gordon and Breach. 1989, 443 pp., $98. - G. Karpilovsky. Unit Groups of Classical Rings. Clarendon Press. 1989, 370 pp., £50. - G. Karpilovsky. Unit Groups of Group Rings. Longman. 1989, 393 pp., £60. - E. Krätzel. Lattice Points. Kluwer Academic Publishers. 1989, 320 pp., £58. - E. Lowen-Colebunders. Function Classes of Cauchy Continuous Maps. Marcel Dekker. 1989, 200 pp., $107.50. - P. S. Milojevic, Editor. Nonlinear Functional Analysis. Marcel Dekker. 1990, 280 pp., $107.50. - D. S. Mitrinović, J. E. Pečarić and V. Volonec. Recent Advances in Geometric Inequalities. Kluwer Academic Publishers. 1989, 710 pp., £90. - P. Nelson, V. Faber, T. Manteuffel, D. L. Seth and A. B. White, Editors. Transport Theory, Invariant Imbedding and Integral Equations. Marcel Dekker. 1989, 480 pp., $132. - M. Ronan. Lectures on Buildings. Academic Press. 1989, 201 pp., $27.95 - S. M. Ross. Introduction to Probability Models, 4th Edition. Academic Press. 1989, 544 pp., $44.50. - D. E. Rowe and J. McCleary, Editors. The History of Modern Mathematics: Vol. I, Ideas and their Reception. Academic Press. 1989, 453 pp., $39.50. - E. O. Roxin, Editor. Modern Optimal Control. Marcel Dekker. 1989, 464 pp., $119.50. - K. D. Schmidt. Jordan Decompositions of Generalized Vector Measures. Longman. 1989, 142 pp., £15. - M. Sharpe. General Theory of Markov Processes. Academic Press. 1988, 419 pp., $49.50. - B. D. Vujanovic and S. E. Jones. Variational Methods in Nonconservative Phenomena. Academic Press. 1989, 370 pp., $59.95. - J. K. Strayer. Linear Programming and its Applications. Springer. 1989, 265 pp., 98DM. - R. Wong. Asymptotic approximation of integrals. Academic Press. 1989, 543 pp., $69.95.
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 143-149
-
- Article
- Export citation
Research Article
Sums of powers of the zeros of the Bessel polynomials
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 305-315
-
- Article
- Export citation
On the dimension of product measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 316-323
-
- Article
- Export citation
Front matter
MTK volume 37 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
A nonparallel cylinder packing with positive density
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 324-331
-
- Article
- Export citation
Book Reviews
BOOK REVIEWS - D. J. Acheson. Elementary Fluid Dynamics. Clarendon Press. 1990, 397 pp., £15. - C. D. Aliprantis and O. Burkinshaw. Principles of Real Analysis. 2nd Edition. Academic Press. 1990, 295 pp., $39.95. - C. D. Aliprantis and O. Burkinshaw. Problems in Real Analysis. Academic Press. 1990, 285 pp., $29.95. - M. Aoki. Optimization of Stochastic Systems: Topics in Discrete-Time Dynamics. Academic Press. 1989, 417 pp., $64.95. - J. Borwein and P. Borwein. A Dictionary of Real Numbers. Wadsworth and Brooks/Cole. 1990, 424 pp., £55-50. - Y. A. Brychkov and A. P. Prudnikov. Integral Transforms of Generalized Functions. Gordon & Breach. 1989, 343 pp., $140. - A. J. Chorin. Computational Fluid Mechanics: Selected Papers. Academic Press. 1989, 223 pp., $35. - C. Clapham. The Concise Oxford Dictionary of Mathematics. Oxford University Press. 1990, 204 pp., £4-95. - P. Constantin and C. Foias. Navier-Stokes Equations. University of Chicago Press. 1988, 190 pp., £27-95. - S. Dineen. The Schwarz Lemma. Clarendon Press. 1989, 248 pp., £25. - P. Dita and V. Georgescu, Editors. Conformal Invariance and String Theory. Academic Press. 1989, 557 pp., $59.95. - L. Eldén and L. Wittmeyer-Koch. Numerical Analysis–an Introduction. Academic Press. 1990, 347 pp., $39.95. - K. D. Elworthy and J.-C. Zambrini. Stochastic Analysis, Path Integration and Dynamics. Longman. 1989, 263 pp., £18. - R. V. Gamkrelidze, Editor. Analysis I: Integral Representations and Asymptotic Methods. Springer. 1989, 238 pp., DM 128. - S. Gelbart and F. Shahidi. Analytic properties of automorphic L-functions. Academic Press. 1988, 131 pp., $18.75. - T. A. Grandine. The Numerical Methods Programming Projects Book. Oxford. 1990, 146 pp., £9-95 - M. H. J. Gruber. Regression Estimators: a Comparative Study. Academic Press. 1990, 347 pp., $49.95. - F. R. Harvey. Spinors and Calibrations. Academic Press. 1990, 313 pp., $39.95. - W. K. Hayman. Subharmonic Functions, Vol. 2. Academic Press. 1989, 590 pp., £53-50. - J. Kevorkian. Partial Differential Equations: Analytical Solution Techniques. Wadsworth and Brooks/Cole. 1990, 547 pp., £14-95. - H.-O. Kreiss and J. Lorenz. Initial-Boundary Value Problems and the Navier Stokes Equations. Academic Press. 1989, 402 pp., $54.50. - S. Lang. A First Course in Calculus. Fifth Edition. Springer. 1986, 280 pp., DM 128. - P. D. Lax and R. S. Phillips. Scattering Theory, 2nd Edition. Academic Press. 1989, 309 pp., $44.95. - J. C. Morgan II. Point set theory. Marcel Dekker. 1990, 296 pp., $119.50. - M. Pavel. Fundamentals of Pattern Recognition. Marcel Dekker. 1989, 183 pp., $107.50. - J. Roitman. Introduction to Modern Set Theory. Wiley. 1990, 156 pp., £32-15. - C. Rogers and W. F. Ames. Nonlinear Boundary Value Problems in Science and Engineering. Academic Press. 1989, 417 pp., $69.9 - D. E. Rowe and J. Mccleary, Editors. The History of Modern Mathematics. Vol. II: Institutions and Applications. Academic Press. 1989, 325 pp., $37.50. - D. Ruelle. Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press. 1989, 187 pp., $27.50 - Y. A. Ryzhov, U. G. Pirumov and V. N. Gorbunov. Nonequilibrium condensation in high-speed gas flows. Gordon and Breach. 1989, 290 pp., $199. - Y. G. Sinai, Editor. Dynamical Systems II. Springer. 1989, 281 pp., DM 128. - V. I. Arnold and S. P. Novikov, Editors. Dynamical Systems IV. Springer. 1990, 283 pp., DM 128. - P. Smith and R. C. Smith. Mechanics. 2nd Edition. Wiley. 1990, 316 pp., £13-95. - G. Stépán. Retarded dynamical systems: stability and characteristic functions. Longman. 1989, 151 pp., £16-50. - G. Toth. Harmonic maps and minimal immersions through representation theory. Academic Press. 1990, 154 pp., $24.95. - M. Vaughan-Lee. The restricted Burnside problem. Oxford University Press. 1990, 209 pp., £27-50. - F. Verhulst. Nonlinear Differential Equations and Dynamical Systems. Springer. 1990, 277 pp., DM38. - A. G. Vitushkin, Editor. Several Complex Variables, I. Springer. 1990, 248 pp., DM128. - W. L. Wood. Practical Time-stepping Schemes. Clarendon Press. 1990, 373 pp., £17-50. - H. S. Wilf. Generating functionology. Academic Press. 1990, 184 pp., $29.95. - M. Young. The Technical Writer's Handbook. Oxford University Press. 1989, 232 pp., £14-95. - E. Zauderer. Partial Differential Equations of Applied Mathematics, 2nd Edition. Wiley. 1989, 891 pp., £51.30 hardback, £29.75 paperback.
-
- Published online by Cambridge University Press:
- 07 April 2017, pp. 332-340
-
- Article
- Export citation
Index
Index to volume 37
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 341
-
- Article
- Export citation
Front matter
MTK volume 37 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
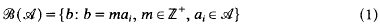
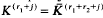 . The conjugates of the number μ in
. The conjugates of the number μ in 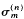 be the sum of the
be the sum of the 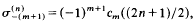
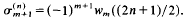
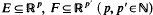 then
then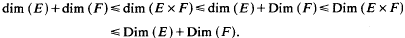
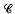 of pairwise disjoint congruent infinite circular cylinders such that no two cylinders of
of pairwise disjoint congruent infinite circular cylinders such that no two cylinders of