This paper depends on results of Baranovskii [1], [2]. The covering radius R(L) of an n-dimensional lattice L is the radius of smallest balls with centres at points of L which cover the whole space spanned by L. R(L) is closely related to minimal vectors of classes of the quotient . The convex hull of all minimal vectors of a class Q is a Delaunay polytope P(Q) of dimension ≤, dimension of L. Let be a maximal squared radius of P(Q) of dimension n (of dimension less than n, respectively). If , then . This is the case in the well-known Barnes-Wall and Leech lattices. Otherwise, . This is a refinement of a result of Norton ([3], Ch. 22).

We show that if the derivative of a convex function on c0 is locally uniformly continuous, then every point x ∈ c0, has a neighbourhood O such that f′(O) is relatively compact in ℓ1.

The following question of V. Stakhovskii was passed to us by N. Dolbilin [4]. Take the barycentric subdivision of a triangle to obtain six triangles, then take the barycentric subdivision of each of these six triangles and so on; is it true that the resulting collection of triangles is dense (up to similarities) in the space of all triangles? We shall show that it is, but that, nevertheless, the process leads almost surely to a flat triangle (that is, a triangle whose vertices are collinear).

The equation

where ℱ is a certain complex-valued function of the given real periodic function λ, is studied analytically and numerically. The equation is motivated physically by a boundary-layer stability problem in which λ represents the skin-friction of the undisturbed basic flow profile. It is proved that no periodic neutral solutions exist for any attached basic flow and the implications of this result for certain vortex-wave interactions are discussed.

A class of mixed type functional differential equations with piecewise constant arguments is studied. The initial value problem is discussed and necessary and sufficient conditions for existence and uniqueness are obtained.

We present a new characterization of σ-fragmentability and illustrate its usefulness by proving some results relating analyticity and crfragmentability. We show, for instance, that a Banach space with the weak topology is σ-fragmented if, and only if, it is almost Čech-analytic and that an almost Čech-analytic topological space is σ-fragmented by a lower-semicontinuous metric if, and only if, each compact subset of the space is fragmented by the metric.

In this paper time-harmonic surface wave motion for progressive waves incident normally on and scattered by a partially immersed fixed vertical barrier in water of infinite depth is considered in the presence of surface tension. The problem for the velocity potential is solved, as others have been previously, by first supposing that the free-surface slopes at the barrier are prescribed and the formal solution in terms of these is obtained explicitly by complex-variable methods. To simplify the calculation the known solution corresponding to zero free-surface slopes at the barrier is subtracted out first and emphasis is placed on determining the residual potential. Finally, an appropriate dynamical edge condition is imposed on the formal solution to determine the required values of the edge-slope constants and hence fully solve the transmission problem. The problem was first examined some time ago using a complex-variable reduction procedure before the advent of this condition, although an explicit formal solution was not obtained, that earlier work forms a basis for the present investigation. It is noted in conclusion how the solution of the problem for waves generated by a partially immersed non-uniform heaving vertical plate may easily be obtained in a similar manner, since the formal solution required is just the residual potential determined in our main problem.

This paper is a contribution to the general problem of differentiability of Lipschitz functions between Banach spaces. We establish here a result concerning the existence of derivatives which are in some sense between the notions of Gâteaux and Frechet differentiability.

Sharp extensions of some classical polynomial inequalities of Bernstein are established for rational function spaces on the unit circle, on K = r (mod 2 π), on [-1, 1 ] and on ℝ. The key result is the establishment of the inequality

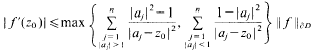
for every rational function f=pn/qn, where pn is a polynomial of degree at most n with complex coefficients and

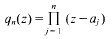
with | aj | ≠ 1 for each j and for every zo∈ δ D, where δ D,= {z∈ ℂ: |z| = l}. The above inequality is sharp at every z0∈δD.

An asymptotic theory is developed for a class of fourth-order differential equations. Under a general conditions on the coefficients of the differential equation we obtained the forms of the asymptotic solutions such that the solutions have different orders of magnitude for large x.

We consider the differential equation

where w(x) = xα for α > -1, q is a real-valued member of (0, ∞) and λ is a complex number with