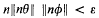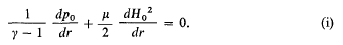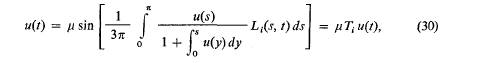Contents
Research Article
An analogue of a problem of Littlewood
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-105
-
- Article
- Export citation
Slow time-dependent motion of a hemisphere in a stratified fluid
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-248
-
- Article
- Export citation
Steady magnetohydrodynamic flow in an insulating circular pipe
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 249-262
-
- Article
- Export citation
On the flow near the trailing edge of a flat plate II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-121
-
- Article
- Export citation
Wing-body interaction in supersonic flow
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 122-142
-
- Article
- Export citation
Triangle models and relations between them
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 263-272
-
- Article
- Export citation
Front matter
MTK volume 16 issue 1 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Neighbourliness and Radon's theorem
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 273-275
-
- Article
- Export citation
Characterization of certain polytopes by intersection properties of their translates
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 276-282
-
- Article
- Export citation
Weber's class invariants
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 283-294
-
- Article
- Export citation
On the steady rotation of an axisymmetric solid in a conducting fluid at high Hartmann numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 295-304
-
- Article
- Export citation
A note on ‘Strong cylindrical shock waves in magnetogasdynamics’
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 305
-
- Article
- Export citation
Corrigendum
Corrigendum: Mathematika Volume 15, 1968
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 306
-
- Article
-
- You have access
- Export citation
Corrigendum: Mathematika Volume 16, 1969
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 307
-
- Article
-
- You have access
- Export citation
Index
Index to volume 16
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 308
-
- Article
- Export citation
Front matter
MTK volume 16 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation