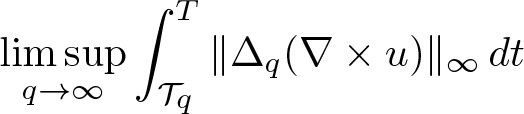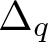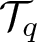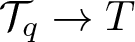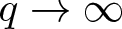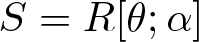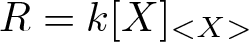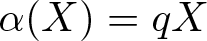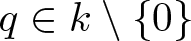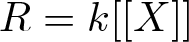FirstView articles
Contents
Research Article
A Negami-type splitting formula for the Jones and Ribbon graph polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the convergence of non-integer linear Hopf flow
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Presymplectic characterization of Liouville sectors with corners, and its monoidality
- Part of:
-
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-71
-
- Article
- Export citation
Corrigendum
Corrigendum: “On the representability of actions of Leibniz algebras and Poisson algebras”
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Research Article
Minimal cobordisms between thin and thick torus knots
-
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelianness and centrality in inverse semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-17
-
- Article
- Export citation
Normalized ground states for a biharmonic Choquard equation with exponential critical growth
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-35
-
- Article
- Export citation
Universal-existential theories of fields
- Part of:
-
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-30
-
- Article
- Export citation
Extended signatures and link concordance
-
- Published online by Cambridge University Press:
- 02 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted Rokhlin property for mapping class groups
- Part of:
-
- Published online by Cambridge University Press:
- 02 September 2025, pp. 1-23
-
- Article
- Export citation
Multiple solutions to relativistic systems with potential boundary conditions
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-14
-
- Article
- Export citation
On coefficient modules of arbitrary modules
- Part of:
-
- Published online by Cambridge University Press:
- 29 August 2025, pp. 1-22
-
- Article
- Export citation
Modified ascent sequences avoiding a pattern of length 4
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-29
-
- Article
- Export citation
G-dimensions for DG-modules over commutative DG-rings
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-20
-
- Article
- Export citation
A study of transcendental entire solutions of several nonlinear partial differential equations
- Part of:
-
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1-41
-
- Article
- Export citation
Mean topological dimension of a random dynamical system for amenable groups
- Part of:
-
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-32
-
- Article
- Export citation
Regularity criteria for the 3D Navier–Stokes and MHD equations
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2025, pp. 1-35
-
- Article
- Export citation
Congruences modulo powers of 5 for partition k-tuples with 5-cores
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2025, pp. 1-17
-
- Article
- Export citation
Elliptic singularities and threefold flops in positive characteristic
- Part of:
-
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-57
-
- Article
- Export citation
Property
 $(\diamond)$ for Ore extensions of small Krull dimension
$(\diamond)$ for Ore extensions of small Krull dimension
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2025, pp. 1-19
-
- Article
- Export citation