Let θ(t, λ) and (t,λ) be the solutions to the differential equation y“+(λ − q(t))y =0, − ∞ <t < ∞ such that θ(0, λ)) = l, θ'(0, λ)) = 0, ø(0, λ) = 0 and ø'(0, λ) = −1. It is known that for a function f(t)∈ L2(−∞,∞), we have
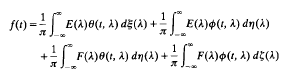
where 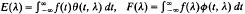 for some measures dξ, dη; and dζ independent of f.
for some measures dξ, dη; and dζ independent of f.
In the first part of this paper we devise a technique to locate the singular points of f(t) (t is complex) under the assumptions that E(λ), F(λ) are of order O(e-cvλ), as λ →∞and q(t) is a sufficiently nice function. In this case all the singularities of fare off the real axis. In the second part of the paper we relax the restriction on E(λ) and f(λ) so that they are of order O(λk) as λ →∞ for some constant k, and we show that in this case f(t) is a generalised function whose analytic representation 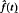 is holomorphic in the upper and lower half planes. We then devise a technique to continue
is holomorphic in the upper and lower half planes. We then devise a technique to continue 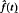 analytically across the real axis and locate its singularities thereon.
analytically across the real axis and locate its singularities thereon.
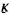 -transformations
-transformations