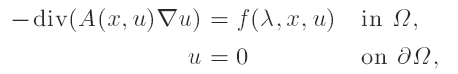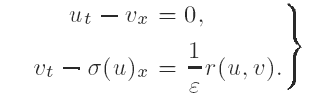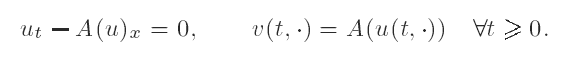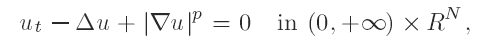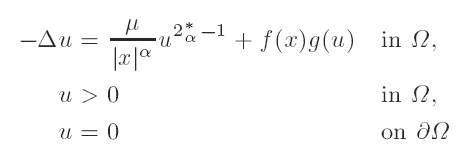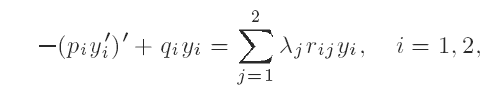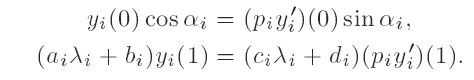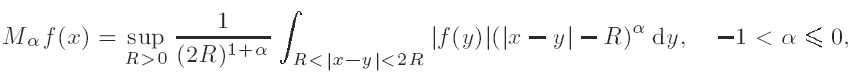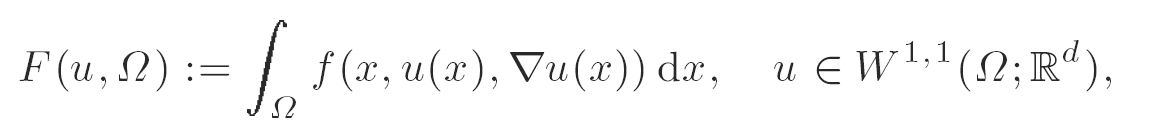Research Article
On a class of two-dimensional singular elliptic problems
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 479-497
-
- Article
- Export citation
Bifurcation for some quasilinear operators
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 733-765
-
- Article
- Export citation
Decay spectrum and decay subspace of normal operators
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1245-1255
-
- Article
- Export citation
Oscillation theory for Sturm–Liouville problems with indefinite coefficients
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 989-1002
-
- Article
- Export citation
On a class of two-dimensional singular elliptic problems
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 479-497
-
- Article
- Export citation
Global BV solutions and relaxation limit for a system of conservation laws
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 1-26
-
- Article
- Export citation
Co-actions of groups
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 225-239
-
- Article
- Export citation
Structure of the Fučík spectrum and existence of solutions for equations with asymmetric nonlinearities
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 241-265
-
- Article
- Export citation
Decay measures on locally compact abelian topological groups
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1257-1273
-
- Article
- Export citation
The deformation multiplicity of a map germ with respect to a Boardman symbol
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1003-1022
-
- Article
- Export citation
Very singular solutions to a nonlinear parabolic equation with absorption. I. Existence
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 27-44
-
- Article
- Export citation
On uniform H2-estimates in periodic homogenization
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 499-517
-
- Article
- Export citation
The classifying space of the gauge group of an SO(3)-bundle over S2
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 767-783
-
- Article
- Export citation
Existence of positive solutions of some semilinear elliptic equations with singular coefficients
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1275-1295
-
- Article
- Export citation
Two-parameter right definite Sturm—Liouville problems with eigenparameter-dependent boundary conditions*
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 45-58
-
- Article
- Export citation
Weighted inequalities for a maximal function on the real line
-
- Published online by Cambridge University Press:
- 11 July 2007, pp. 267-277
-
- Article
- Export citation
On lower semicontinuity and relaxation
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 519-565
-
- Article
- Export citation
Nonlinear elliptic problems on singularly perturbed domains
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1023-1037
-
- Article
- Export citation
The spectral boundary of complemented invariant subspaces in Lp(R)
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 785-798
-
- Article
- Export citation
On uniform H2-estimates in periodic homogenization
-
- Published online by Cambridge University Press:
- 12 July 2007, pp. 499-517
-
- Article
- Export citation