We develop Weyl differencing and Hua-type lemmata for a class of multidimensional exponential sums. We then apply our estimates to bound the number of variables required to establish an asymptotic formula for the number of solutions of a system of diophantine equations arising from the study of linear spaces on hypersurfaces. For small values of the degree and dimension, our results are superior to those stemming from the author’s earlier work on Vinogradov’s mean value theorem.

Paucity is established for a system of diagonal diophantine equations, in which the degrees are the odd numbers in ascending order.

We study the distribution of the size of Selmer groups and Tate–Shafarevich groups arising from a 2-isogeny and its dual 2-isogeny for elliptic curves En:y2=x3−n3. We show that the 2-ranks of these groups all follow the same distribution. The result also implies that the mean value of the 2-rank of the corresponding Tate–Shafarevich groups for square-free positive integers n≤X is as X→∞. This is quite different from quadratic twists of elliptic curves with full 2-torsion points over ℚ [M. Xiong and A. Zaharescu, Distribution of Selmer groups of quadratic twists of a family of elliptic curves. Adv. Math. 219 (2008), 523–553], where one Tate–Shafarevich group is almost always trivial while the other is much larger.

Let a be an integer different from 0, ±1, or a perfect square. We consider a conjecture of Erdős which states that #{p:ℓa(p)=r}≪εrε for any ε>0, where ℓa(p) is the order of a modulo p. In particular, we see what this conjecture says about Artin’s primitive root conjecture and compare it to the generalized Riemann hypothesis and the ABC conjecture. We also extend work of Goldfeld related to divisors of p+a and the order of a modulo p.

Extending classical results of Nair and Tenenbaum, we provide general, sharp upper bounds for sums of the type 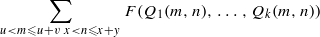where x,y,u,v have comparable logarithms, F belongs to a class defined by a weak form of sub-multiplicativity, and the Qj are arbitrary binary forms. A specific feature of the results is that the bounds are uniform within the F-class and that, as in a recent version given by Henriot, the dependency with respect to the coefficients of the Qj is made explicit. These estimates play a crucial rôle in the proof, published separately by the authors, of Manin’s conjecture for Châtelet surfaces.

Let T be an algebraic torus over ℚ such that T(ℝ) is compact. Assuming the generalized Riemann hypothesis, we give a lower bound for the size of the class group of T modulo its n-torsion in terms of a small power of the discriminant of the splitting field of T. As a corollary, we obtain an upper bound on the n-torsion in that class group. This generalizes known results on the structure of class groups of complex multiplication fields.

The paper extends the fundamental existence assertion for probability contents and measures with given marginals: the extension is from algebras to lattices, and thus is in accord with an actual trend in measure and integration. The proof of the basic theorem is a rapid application of a former Hahn–Banach type separation theorem.

We consider uniformly elliptic operators with Dirichlet or Neumann homogeneous boundary conditions on a domain Ω in ℝN. We consider deformations ϕ(Ω) of Ω obtained by means of a locally Lipschitz homeomorphism ϕ and we estimate the variation of the eigenfunctions and eigenvalues upon variation of ϕ. We prove general stability estimates without assuming uniform upper bounds for the gradients of the maps ϕ. As an application, we obtain estimates on the rate of convergence for eigenvalues and eigenfunctions when a domain with an outward cusp is approximated by a sequence of Lipschitz domains.

We suggest an alternative mathematical model for the electron in dimension 1+2. We think of our (1+2)-dimensional spacetime as an elastic continuum whose material points can experience no displacements, only rotations. This framework is a special case of the Cosserat theory of elasticity. Rotations of material points are described mathematically by attaching to each geometric point an orthonormal basis which gives a field of orthonormal bases called the coframe. As the dynamical variables (unknowns) of our theory we choose a coframe and a density. We then add an extra (third) spatial dimension, extend our coframe and density into dimension 1+3, choose a conformally invariant Lagrangian proportional to axial torsion squared, roll up the extra dimension into a circle so as to incorporate mass and return to our original (1+2)-dimensional spacetime by separating out the extra coordinate. The main result of our paper is the theorem stating that our model is equivalent to the Dirac equation in dimension 1+2. In the process of analysing our model we also establish an abstract result, identifying a class of nonlinear second order partial differential equations which reduce to pairs of linear first order equations.

For q>1, the set Fq of real numbers which can be expanded in base q with respect to the digit set {0,1,q} is just a self-similar set with overlaps. We consider the subset of Fq whose elements have a unique expansion and calculate its Hausdorff dimension for the case where .

We study the question of whether every centred convex body K of volume 1 in ℝn has “supergaussian directions”, which means θ∈Sn−1 such that for all , where c>0 is an absolute constant. We verify that a “random” direction is indeed supergaussian for isotropic convex bodies that satisfy the hyperplane conjecture. On the other hand, we show that if, for all isotropic convex bodies, a random direction is supergaussian then the hyperplane conjecture follows.

In 1946 Erdős asked for the maximum number of unit distances, u(n), among n points in the plane. He showed that u(n)>n1+c/log log n and conjectured that this was the true magnitude. The best known upper bound is u(n)<cn4/3, due to Spencer, Szemerédi and Trotter. We show that the upper bound holds if we only consider unit distances with rational angle, by which we mean that the line through the pair of points makes a rational angle in degrees with the x-axis. Using an algebraic theorem of Mann we get a uniform bound on the number of paths between two fixed vertices in the unit distance graph, giving a contradiction if there are too many unit distances with rational angle. This bound holds if we consider rational distances instead of unit distances as long as there are no three points on a line. A superlinear lower bound is given, due to Erdős and Purdy. If we have at most nα points on a line then we get the bound O(n1+α) or for the number of rational distances with rational angle depending on whether α≥1/2 or α<1/2 respectively.

We introduce a precise framework for transferring strategies from simpler to more complex games, and use it to construct strategies in certain finite and infinite combinations of games. In particular, we give a finitary characterization of finite hypergraphs X such that the first player can win the positional game on infinitely many copies of X. This resolves a conjecture of Leader.