Simulations of steady two-dimensional stratified flow over an isolated obstacle are presented where the obstacle is tall enough so that the topographic Froude number, Nhm/Uo ≫ 1. N is the buoyancy frequency, hm the height of the topography from the channel floor and Uo the flow speed infinitely far from the obstacle. As for moderate Nhm/Uo (~1), a columnar response propagates far up- and downstream, and an arrested lee wave forms at the topography. Upstream, most of the water beneath the crest is blocked, while the moving layer above the crest has a mean velocity Um = UoH/(H−hm). The vertical wavelength implied by this velocity scale, λo = 2πUm/N, predicts dominant vertical scales in the flow. Upstream of the crest there is an accelerated region of fluid approximately λo thick, above which there is a weakly oscillatory flow. Downstream the accelerated region is thicker and has less intense velocities. Similarly, the upstream lift of isopycnals is greatest in the first wavelength near the crest, and weaker above and below. Form drag on the obstacle is dominated by the blocked response, and not on the details of the lee wave, unlike flows with moderate Nhm/Uo.
Directly downstream, the lee wave that forms has a vertical wavelength given by λo, except for the deepest lobe which tends to be thicker. This wavelength is small relative to the fluid depth and topographic height, and has a horizontal phase speed cpx = −Um, corresponding to an arrested lee wave. When considering the spin-up to steady state, the speed of vertical propagation scales with the vertical component of group velocity cgz = αUm, where α is the aspect ratio of the topography. This implies a time scale 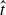 = tNα/2π for the growth of the lee waves, and that steady state is attained more rapidly with steep topography than shallow, in contrast with linear theory, which does not depend on the aspect ratio.
= tNα/2π for the growth of the lee waves, and that steady state is attained more rapidly with steep topography than shallow, in contrast with linear theory, which does not depend on the aspect ratio.