Recent fraud cases in psychological and medical research have emphasized the need to pay attention to Questionable Research Practices (QRPs). Deliberate or not, QRPs usually have a deteriorating effect on the quality and the credibility of research results. QRPs must be revealed but prevention of QRPs is more important than detection. I suggest two policy measures that I expect to be effective in improving the quality of psychological research. First, the research data and the research materials should be made publicly available so as to allow verification. Second, researchers should more readily consider consulting a methodologist or a statistician. These two measures are simple but run against common practice to keep data to oneself and overestimate one’s methodological and statistical skills, thus allowing secrecy and errors to enter research practice.

We comment on Sijtsma’s (2014) thought-provoking essay on how to minimize questionable research practices (QRPs) in psychology. We agree with Sijtsma that proactive measures to decrease the risk of QRPs will ultimately be more productive than efforts to target individual researchers and their work. In particular, we concur that encouraging researchers to make their data and research materials public is the best institutional antidote against QRPs, although we are concerned that Sijtsma’s proposal to delegate more responsibility to statistical and methodological consultants could inadvertently reinforce the dichotomy between the substantive and statistical aspects of research. We also discuss sources of false-positive findings and replication failures in psychological research, and outline potential remedies for these problems. We conclude that replicability is the best metric of the minimization of QRPs and their adverse effects on psychological research.

We respond to the commentaries Waldman and Lilienfeld (Psychometrika, 2015) and Wigboldus and Dotch (Psychometrika, 2015) provided in response to Sijtsma’s (Sijtsma in Psychometrika, 2015) discussion article on questionable research practices. Specifically, we discuss the fear of an increased dichotomy between substantive and statistical aspects of research that may arise when the latter aspects are laid entirely in the hands of a statistician, remedies for false positives and replication failure, and the status of data exploration, and we provide a re-definition of the concept of questionable research practices.

When a simple sum or number-correct score is used to evaluate the ability of individual testees, then, from an accountability perspective, the inferences based on the sum score should be the same as the inferences based on the complete response pattern. This requirement is fulfilled if the sum score is a sufficient statistic for the parameter of a unidimensional model. However, the models for which this holds true are known to be restrictive. It is shown that the less restrictive nonparametric models could result in an ordering of persons that is different from an ordering based on the sum score. To arrive at a fair evaluation of ability with a simple number-correct score, ordinal sufficiency is defined as a minimum condition for scoring. The monotone homogeneity model, together with the property of ordinal sufficiency of the sum score, is introduced as the nonparametric Rasch model. A basic outline for testable hypotheses about ordinal sufficiency, as well as illustrations with real data, is provided.

In planned missingness (PM) designs, certain data are set a priori to be missing. PM designs can increase validity and reduce cost; however, little is known about the loss of efficiency that accompanies these designs. The present paper compares PM designs to reduced sample (RN) designs that have the same total number of data points concentrated in fewer participants. In 4 studies, we consider models for both observed and latent variables, designs that do or do not include an “X set” of variables with complete data, and a full range of between- and within-set correlation values. All results are obtained using asymptotic relative efficiency formulas, and thus no data are generated; this novel approach allows us to examine whether PM designs have theoretical advantages over RN designs removing the impact of sampling error. Our primary findings are that (a) in manifest variable regression models, estimates of regression coefficients have much lower relative efficiency in PM designs as compared to RN designs, (b) relative efficiency of factor correlation or latent regression coefficient estimates is maximized when the indicators of each latent variable come from different sets, and (c) the addition of an X set improves efficiency in manifest variable regression models only for the parameters that directly involve the X-set variables, but it substantially improves efficiency of most parameters in latent variable models. We conclude that PM designs can be beneficial when the model of interest is a latent variable model; recommendations are made for how to optimize such a design.

Mean corrected higher order sample moments are asymptotically normally distributed. It is shown that both in the literature and popular software the estimates of their asymptotic covariance matrices are incorrect. An introduction to the infinitesimal jackknife is given and it is shown how to use it to correctly estimate the asymptotic covariance matrices of higher order sample moments. Another advantage in using the infinitesimal jackknife is the ease with which it may be used when stacking or sub-setting estimators. The estimates given are used to test the goodness of fit of a non-linear factor analysis model. A computationally accelerated form for infinitesimal jackknife estimates is given.

The past decade has evidenced the increased prevalence of irregularly spaced longitudinal data in social sciences. Clearly lacking, however, are modeling tools that allow researchers to fit dynamic models to irregularly spaced data, particularly data that show nonlinearity and heterogeneity in dynamical structures. We consider the issue of fitting multivariate nonlinear differential equation models with random effects and unknown initial conditions to irregularly spaced data. A stochastic approximation expectation–maximization algorithm is proposed and its performance is evaluated using a benchmark nonlinear dynamical systems model, namely, the Van der Pol oscillator equations. The empirical utility of the proposed technique is illustrated using a set of 24-h ambulatory cardiovascular data from 168 men and women. Pertinent methodological challenges and unresolved issues are discussed.

In forced-choice questionnaires, respondents have to make choices between two or more items presented at the same time. Several IRT models have been developed to link respondent choices to underlying psychological attributes, including the recent MUPP (Stark et al. in Appl Psychol Meas 29:184–203, 2005) and Thurstonian IRT (Brown and Maydeu-Olivares in Educ Psychol Meas 71:460–502, 2011) models. In the present article, a common framework is proposed that describes forced-choice models along three axes: (1) the forced-choice format used; (2) the measurement model for the relationships between items and psychological attributes they measure; and (3) the decision model for choice behavior. Using the framework, fundamental properties of forced-choice measurement of individual differences are considered. It is shown that the scale origin for the attributes is generally identified in questionnaires using either unidimensional or multidimensional comparisons. Both dominance and ideal point models can be used to provide accurate forced-choice measurement; and the rules governing accurate person score estimation with these models are remarkably similar.

A new Bayesian multinomial probit model is proposed for the analysis of panel choice data. Using a parameter expansion technique, we are able to devise a Markov Chain Monte Carlo algorithm to compute our Bayesian estimates efficiently. We also show that the proposed procedure enables the estimation of individual level coefficients for the single-period multinomial probit model even when the available prior information is vague. We apply our new procedure to consumer purchase data and reanalyze a well-known scanner panel dataset that reveals new substantive insights. In addition, we delineate a number of advantageous features of our proposed procedure over several benchmark models. Finally, through a simulation analysis employing a fractional factorial design, we demonstrate that the results from our proposed model are quite robust with respect to differing factors across various conditions.

This paper focuses on the computation of asymptotic standard errors (ASE) of ability estimators with dichotomous item response models. A general framework is considered, and ability estimators are defined from a very restricted set of assumptions and formulas. This approach encompasses most standard methods such as maximum likelihood, weighted likelihood, maximum a posteriori, and robust estimators. A general formula for the ASE is derived from the theory of M-estimation. Well-known results are found back as particular cases for the maximum and robust estimators, while new ASE proposals for the weighted likelihood and maximum a posteriori estimators are presented. These new formulas are compared to traditional ones by means of a simulation study under Rasch modeling.

Stevens’ power law for the judgments of sensation has a long history in psychology and is used in many psychophysical investigations of the effects of predictors such as group or condition. Stevens’ formulation $\mathit{\Psi }={aP}^n$\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varPsi = {aP}^{n}$$\end{document}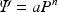, where $\mathit{\Psi }$\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$\varPsi $$\end{document} 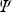is the psychological judgment, P is the physical intensity, and $n$\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$n$$\end{document} is the power law exponent, is usually tested by plotting log $(\mathit{\Psi })$\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$(\varPsi )$$\end{document}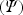 against log (P). In some, but by no means all, studies, effects on the scale parameter, $a$\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$a$$\end{document}, are also investigated. This two-parameter model is simple but known to be flawed, for at least some modalities. Specifically, three-parameter functions that include a threshold parameter produce a better fit for many data sets. In addition, direct non-linear computation of power laws often fit better than regressions of log-transformed variables. However, such potentially flawed methods continue to be used because of assumptions that the approximations are “close enough” as to not to make any difference to the conclusions drawn (or possibly through ignorance the errors in these assumptions). We investigate two modalities in detail: duration and roughness. We show that a three-parameter power law is the best fitting of several plausible models. Comparison between this model and the prevalent two parameter version of Stevens’ power law shows significant differences for the parameter estimates with at least medium effect sizes for duration.

Intensive longitudinal data provide rich information, which is best captured when specialized models are used in the analysis. One of these models is the multilevel autoregressive model, which psychologists have applied successfully to study affect regulation as well as alcohol use. A limitation of this model is that the autoregressive parameter is treated as a fixed, trait-like property of a person. We argue that the autoregressive parameter may be state-dependent, for example, if the strength of affect regulation depends on the intensity of affect experienced. To allow such intra-individual variation, we propose a multilevel threshold autoregressive model. Using simulations, we show that this model can be used to detect state-dependent regulation with adequate power and Type I error. The potential of the new modeling approach is illustrated with two empirical applications that extend the basic model to address additional substantive research questions.