In this paper we prove a boundedness theorem in the theory ID1(W). This answers a question asked by Feferman, for example in [3]. The background is the following.
Let A[X, x] be an X-positive formula arithmetic in X. The theory ID1(PA) is an extension of Peano arithmetic PA by the following axioms:
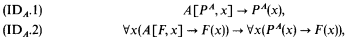
for arbitrary formulas F; PA is a constant for the least fixed point of A[X, x]. Set-theoretically, PA can be defined by recursion on the ordinals as follows:
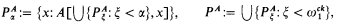
where 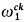 is the first nonrecursive ordinal.
is the first nonrecursive ordinal.
Now let a ≺ b be the arithmetic relation which expresses that the recursive tree coded by a is a proper subtree of the tree coded by b, and define
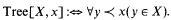
The least fixed point of Tree[X, x] is the set PTree of all well-founded recursive trees. We write W or Wα for PTree or 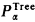 , respectively. Since W is
, respectively. Since W is 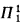 complete we have
complete we have 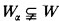 for all α <
for all α < 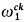 . If we define for each element a ∈ W its inductive norm ∣a∣ by ∣a∣≔ min{ξ: a ∈ Wξ}, then we have
. If we define for each element a ∈ W its inductive norm ∣a∣ by ∣a∣≔ min{ξ: a ∈ Wξ}, then we have 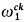 = {∣a∣: a ∈ W} and the elements of W can be used as codes for the ordinals less than
= {∣a∣: a ∈ W} and the elements of W can be used as codes for the ordinals less than 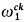 .
.
Assume that B[X, x] is an X-positive formula arithmetic in X with the only free variables X and x, and assume that QB is a relation that satisfies
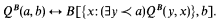
If we define
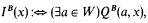
then we obviously have PB = IB.