Research Article
Geometry of *-Finite Types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1375-1395
-
- Article
- Export citation
Lowness for the class of random sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1396-1402
-
- Article
- Export citation
Friedberg splittings in Σ30 quotient lattices of

-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1403-1406
-
- Article
- Export citation
Interpretability over peano arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1407-1425
-
- Article
- Export citation
Ordre fondamental d'une théorie 1-basée
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1426-1438
-
- Article
- Export citation
Quine's ‘limits of decision’
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1439-1466
-
- Article
- Export citation
A model with no magic set
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1467-1490
-
- Article
- Export citation
On the No-Counterexample Interpretation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1491-1511
-
- Article
- Export citation
Cantor-Bendixson Rank of the Ziegler Spectrum Over a Commutative Valuation Domain
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1512-1518
-
- Article
- Export citation
The Complexity of the Collection of Countable Linear Orders of the form I + I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1519-1526
-
- Article
- Export citation
Cardinal preserving ideals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1527-1551
-
- Article
- Export citation
Finite sets and frege structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1552-1556
-
- Article
- Export citation
A Note on a-Prime Models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1557-1562
-
- Article
- Export citation
Decidability of cylindric set algebras of dimension two and first-order logic with two variables
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1563-1572
-
- Article
- Export citation
Displaying the modal logic of consistency
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1573-1590
-
- Article
- Export citation
No elementary embedding from v into v is definable from parameters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1591-1594
-
- Article
- Export citation
Stable models and reflexive banach spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1595-1600
-
- Article
- Export citation
A minimal counterexample to universal baireness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1601-1627
-
- Article
- Export citation
A hierarchy of maps between compacta
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1628-1644
-
- Article
- Export citation
Standardization principle of nonstandard universes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1645-1655
-
- Article
- Export citation

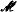 -rank > 0 is m-nonorthogonal to a *-algebraic type of
-rank > 0 is m-nonorthogonal to a *-algebraic type of 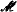 -rank 1. We study the geometry induced by m-dependence on a *-algebraic type
-rank 1. We study the geometry induced by m-dependence on a *-algebraic type 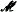 -rank 1. We prove that after some localization this geometry becomes projective over a division ring
-rank 1. We prove that after some localization this geometry becomes projective over a division ring 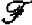 . Associated with
. Associated with 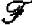 underlies also the geometry induced by forking dependence on any stationarization of
underlies also the geometry induced by forking dependence on any stationarization of 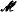 -rank 1 and prove that any *-algebraic *-group of
-rank 1 and prove that any *-algebraic *-group of 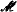 -rank 1 is abelian-by-finite.
-rank 1 is abelian-by-finite.
 set, then we can define a
set, then we can define a 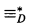 by putting W
by putting W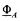 of order type < ε
of order type < ε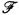 of subsets of a set
of subsets of a set 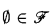 and
and 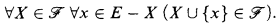
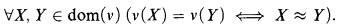
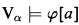 .”
.”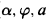 expresses the satisfaction relation
expresses the satisfaction relation 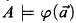 . The formula Fmla(
. The formula Fmla(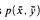 .
.