 $\ell $-REGULAR NONOVERLINED PARTS
$\ell $-REGULAR NONOVERLINED PARTS
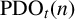 $\text {PDO}_t(n)$ BY POWERS OF
$\text {PDO}_t(n)$ BY POWERS OF 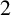 $2$ AND
$2$ AND 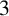 $3$
$3$
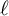 $\ell $
-core index
$\ell $
-core index
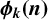 $\boldsymbol {\phi _k(n)}$
$\boldsymbol {\phi _k(n)}$