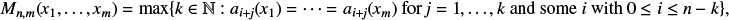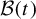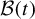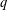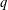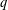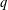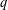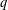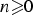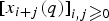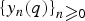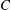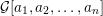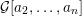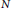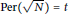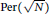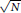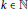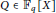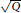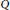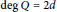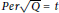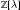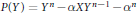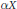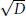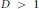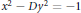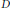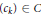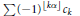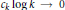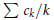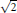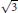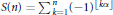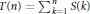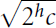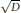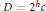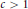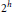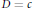25 results
Equality cases of the Alexandrov–Fenchel inequality are not in the polynomial hierarchy
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SHORTEST DISTANCE FUNCTION IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 186-195
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Dilogarithm identities after Bridgeman
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 03 March 2022, pp. 1-23
- Print publication:
- January 2023
-
- Article
- Export citation
POINTS IN A FOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 7-17
- Print publication:
- August 2022
-
- Article
- Export citation
The bifurcation locus for numbers of bounded type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2239-2269
- Print publication:
- July 2022
-
- Article
- Export citation
THE ROGERS–RAMANUJAN CONTINUED FRACTION AND RELATED ETA-QUOTIENT REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 248-259
- Print publication:
- April 2021
-
- Article
- Export citation
AN EXACT FORMULA FOR THE HARMONIC CONTINUED FRACTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 11-21
- Print publication:
- February 2021
-
- Article
- Export citation
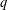 $q$-DEFORMED RATIONALS AND
$q$-DEFORMED RATIONALS AND 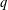 $q$-CONTINUED FRACTIONS
$q$-CONTINUED FRACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation
Positivity and continued fractions from the binomial transformation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 18 March 2019, pp. 831-847
- Print publication:
- June 2019
-
- Article
- Export citation
Numbers with Almost all Convergents in a Cantor Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 869-875
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Distribution of Class Numbers in Continued Fraction Families of Real Quadratic Fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 20 August 2018, pp. 1193-1212
-
- Article
- Export citation
Cluster algebras and continued fractions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 22 December 2017, pp. 565-593
- Print publication:
- March 2018
-
- Article
- Export citation
On the Continued Fraction Expansion of Fixed Period in Finite Fields
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 704-712
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation
Conjugacy Classes and Binary Quadratic Forms for the Hecke Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 3 / 01 September 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 570-583
- Print publication:
- 01 September 2013
-
- Article
-
- You have access
- Export citation
The Smallest Pisot Element in the Field of Formal Power Series Over a Finite Field
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-264
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Pell Equations: Non-Principal Lagrange Criteria and Central Norms
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 774-782
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
An AF Algebra Associated with the Farey Tessellation
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 975-1000
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
On the Convergence of a Class of Nearly Alternating Series
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 1 / 01 February 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 85-108
- Print publication:
- 01 February 2007
-
- Article
-
- You have access
- Export citation
RECURRENCE RELATIONS FOR ELLIPTIC SEQUENCES: EVERY SOMOS 4 IS A SOMOS LOWERCASE $k$
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 4 / August 2006
- Published online by Cambridge University Press:
- 24 July 2006, pp. 546-554
- Print publication:
- August 2006
-
- Article
- Export citation
Necessary and Sufficient Conditions for the Central Norm to Equal 2h in the Simple Continued Fraction Expansion of
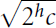 $\sqrt{{{2}^{h}}c}$
$\sqrt{{{2}^{h}}c}$
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 1 / 01 March 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 121-132
- Print publication:
- 01 March 2005
-
- Article
-
- You have access
- Export citation